简介
什么是卡诺图?
您是否好奇计算机如何做决策?它们使用一种称为布尔逻辑的系统,处理真与假的值。当这些真假陈述组合起来时可能变得非常复杂,这时卡诺图(K-Map)就派上用场了。卡诺图是一种将逻辑陈述整理成清晰网格的工具,这个网格展示所有可能的变量组合,让我们快速识别模式。发现这些模式有助于简化逻辑表达式。
若想深入了解K-Map原理或四变量K-Map解法,请参考技术文章获取详细信息: 如何解决四变量K-Map问题
为什么使用五变量卡诺图?
常规卡诺图处理二、三或四个变量,但当面对五个变量的复杂系统时——比如设计带五个开关的电路(每个开关都有开/关状态)——五变量卡诺图就显示出优势。它能简化原本难以处理的表达式,无论是硬件设计还是软件开发都能节省大量时间。
五变量卡诺图结构解析
布局与变量分配
五变量卡诺图本质上是四变量版本的扩展。四变量图采用4x4网格(16单元格),行用B/C变量,列用D/E变量。增加第五变量A后,我们使用两个并置的4x4网格(共32单元格)——左侧网格表示A=0,右侧表示A=1。每个网格内仍保持B/C行、D/E列的格雷码排序,既保留熟悉结构又扩展了变量容量。

与四变量图的差异
主要区别体现在:
- 单元格倍增:32单元格满足五变量组合需求
- 双网格架构:通过A=0/A=1区分两个网格
- 跨网格邻接:相同位置的单元格在A=0/A=1网格间互为邻接
- 更大组群:支持最多32单元格的组群(但常用较小规模)
核心的分组逻辑与四变量图保持一致
五变量卡诺图构建指南
步骤一:确定变量
选定五个变量(如A,B,C,D,E),明确布尔函数在各组合下的真值(1/0)。
步骤二:行列标注
采用格雷码标注:行使用B/C(00,01,11,10),列使用D/E(相同排序),左网格标记A=0,右网格A=1。
步骤三:填充真值
根据变量组合的真值结果,在对应网格位置填写1/0。若已知最小项(minterms),直接在对应单元格填1。
五变量卡诺图分组策略
分组规则
通过分组1单元格进行简化,规则包括:
- 组大小必须为2的幂(1,2,4,8,16,32)
- 组形应为矩形或正方形
- 仅邻接单元格可成组
- 优先最大可能分组
- 每个1至少属于一个组

识别邻接单元格
邻接指仅一个变量不同的单元格。除网格内水平/垂直邻接外,A=0/A=1网格的相同位置单元格互为邻接。例如A=0网格的B'C'D'E'与A=1网格的同位置单元格可形成跨网格组。
处理循环边界
卡诺图具有环形拓扑特性:网格上下边缘相连,左右边缘相连,同时支持跨网格邻接。这种特性使得分组可跨越传统边界,形成更优化的组群。

布尔表达式简化方法
寻找主蕴含项
主蕴含项指无法再扩大的最大有效组。通过穷尽所有可能分组,筛选出不可合并的组作为简化基础。
选择必要主蕴含项
必要主蕴含项覆盖唯一包含某个1的分组。优先选择这些组,再补充覆盖剩余1的非必要组。
构建最简表达式
每组生成一个与项:
- 识别组内恒定变量
- 恒定1的变量保留原形(如B)
- 恒定0的变量取反(如B')
- 忽略变化变量
最终表达式为各与项的或运算组合。

五变量卡诺图实例解析
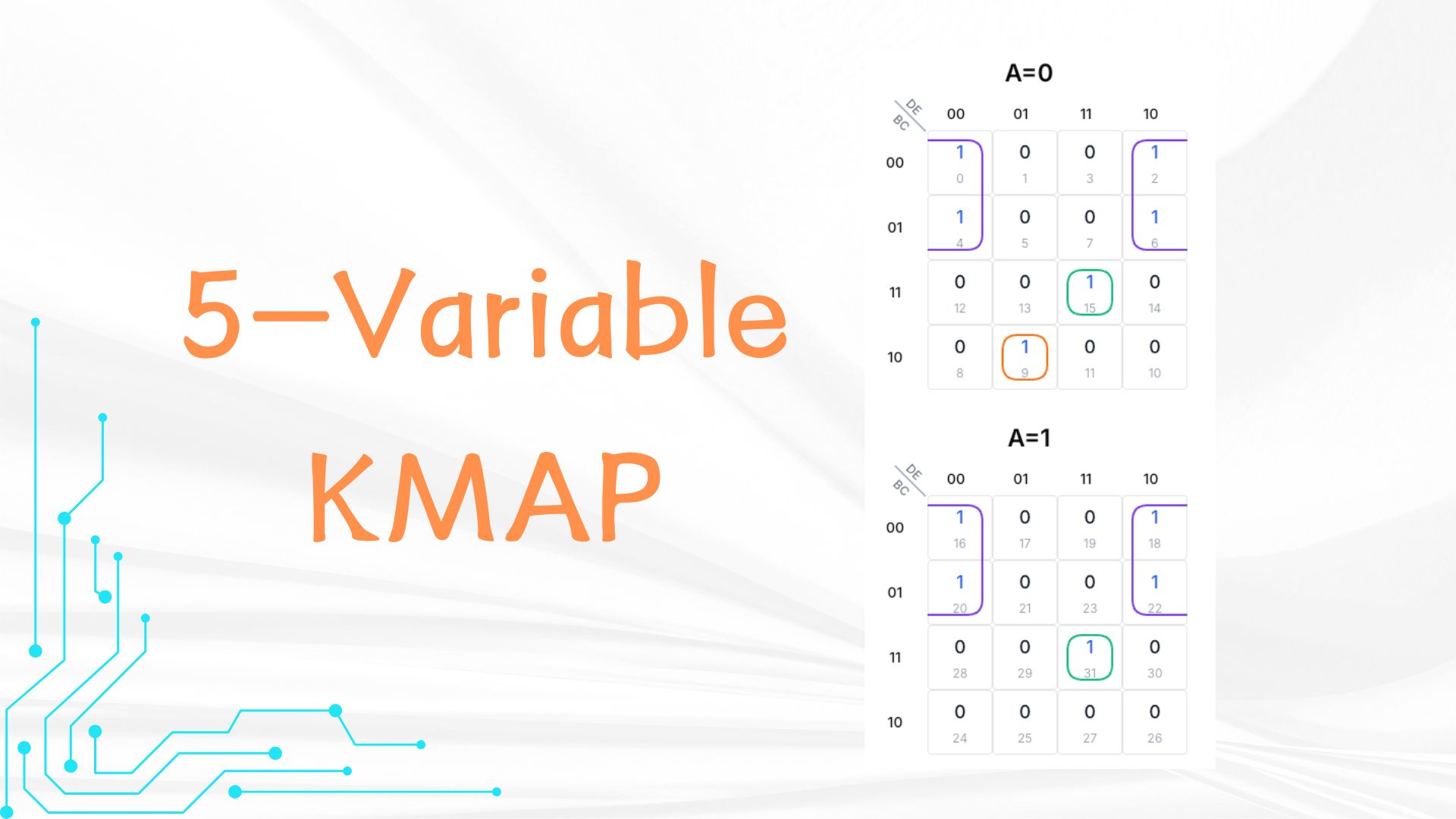
示例表达式:A'B'C'D'E' + A'B'C'DE' + A'B'CD'E' + A'B'CDE' + A'BC'D'E + A'BCDE + AB'C'D'E' + AB'C'DE' + AB'CD'E' + AB'CDE' + ABCDE,对应二进制位置:0,2,4,6,9,15,16,18,20,22,31。
步骤一:填充真值
A=0网格填充:
- 行00列00:1
- 行00列01:1
- 行01列11:1
- 行01列10:1
- 行11列11:1
- 行10列01:1
In the A=1 grid, rows are also B and C (00, 01, 11, 10), columns are also D and E (00, 01, 11, 10). Put 1s:
- 行00列00:1
- 行00列01:1
- 行01列11:1
- 行01列10:1
- 行11列11:1

步骤二:分组优化
11个1值分布:A=0网格6个,A=1网格5个
- 组1:单一项A'BC'D'E
- 组2:跨网格B'E'组
- 组3:BCDE跨A组

步骤三:表达式生成
- 组1保留:A'BC'D'E
- 组2简化为:B'E'
- 组3简化为:BCDE
最简表达式:A'BC'D'E + B'E' + BCDE

五变量卡诺图精要指南
常见误区
- 错误标注:未使用格雷码导致邻接错误
- 遗漏连接:忽视跨网格邻接可能
- 无效分组:包含非邻接单元格
- 保守分组:未最大化组规模
- 变量误判:错误识别恒定变量
高效实践准则
- 严格采用格雷码标注
- 优先构建最大可能组
- 系统检查跨网格组合
- 确保全覆盖所有1值
- 通过网格位置验证项准确性
立即通过我们的 交互式K-Map求解工具 实践五变量卡诺图解法,该工具支持最多五变量输入,是验证方案和提升技能的理想选择。