四变量K-Map求解指南：清晰易懂的实用教程

什么是K-Map及其在数字逻辑中的作用

K-Map（卡诺图）是简化数字逻辑中布尔表达式的可视化工具。这些表达式如同数字电路的指令，通过真值与假值将输入转换为输出。简化后的表达式能使电路更小、更快且成本更低。

卡诺图通过网格实现简化。在四变量图中，16个单元格分别代表四个输入变量的独特组合。相邻单元格仅有一个变量不同，这种排列便于识别模式并分组相似输出。

卡诺图的优势在于直观易用，相比纯数学方法更能减少错误。它特别适合四到五变量的场景，完美契合实际电路设计需求。

理解网格与变量分配

四变量卡诺图始于4×4网格，16个单元格对应A、B、C、D四个变量的所有可能组合。行标签使用AB变量对，列标签使用CD变量对。根据逻辑问题填写1或0，将抽象问题转化为可视化模型。

四变量K-Map网格及单元格编号（最小项）

格雷码在卡诺图中的重要性

观察四变量卡诺图的行列标签：它们不采用常规二进制序列00、01、10、11，而是使用格雷码00、01、11、10。格雷码每次仅改变一个比特，例如01到11仅首比特变化。

这种编码至关重要。格雷码确保相邻单元格仅有一个变量不同，使表达式简化的分组操作变得直观。若采用普通二进制编码，分组将变得复杂困难。

将布尔函数转换为最小项

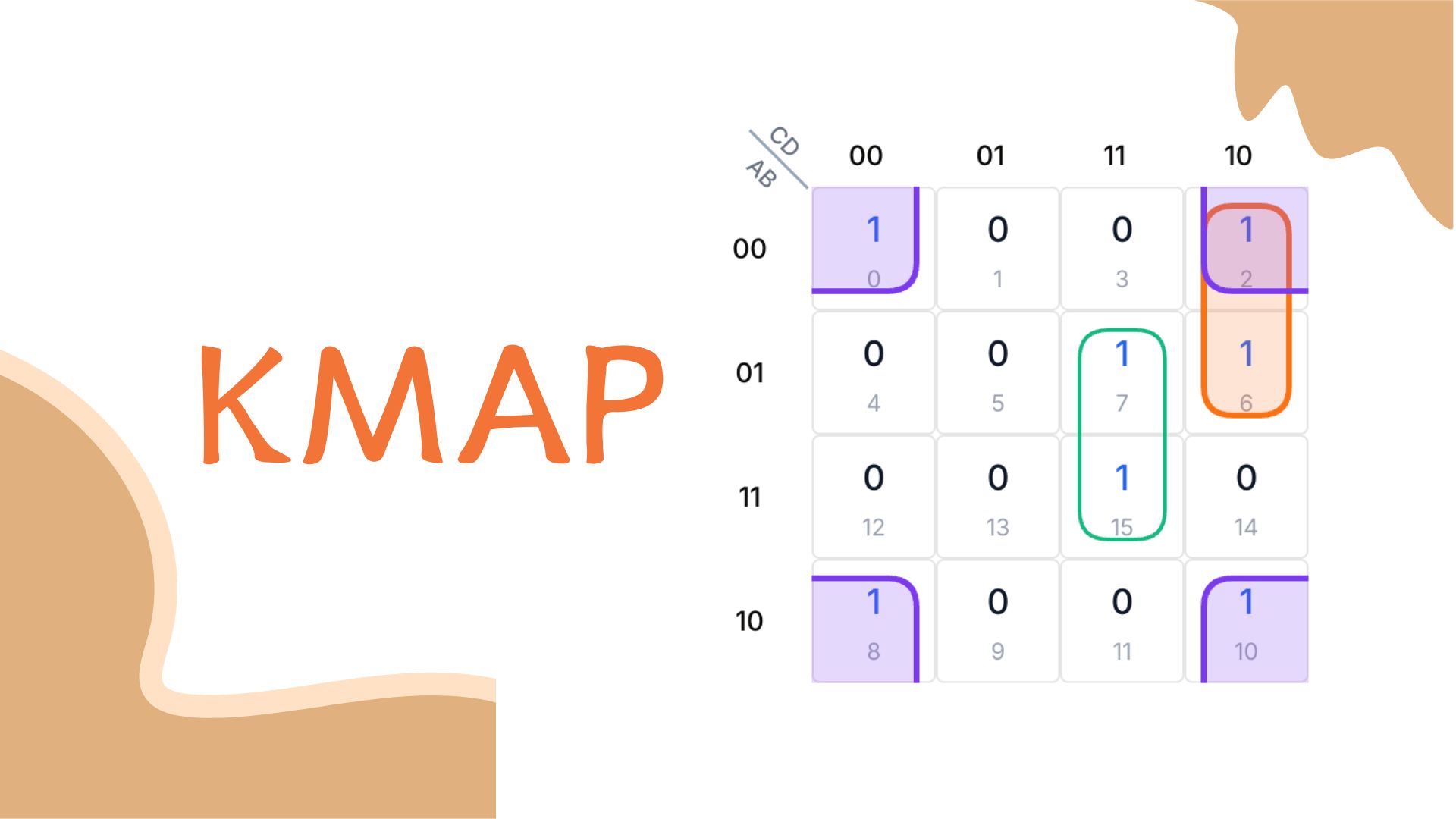
使用四变量卡诺图时，首先确定使布尔函数为真的输入组合——即最小项。以函数F = A'B'C'D' + A'B'CD' + A'BC'D + A'BCD + AB'C'D' + AB'CD'为例，每个项对应特定变量组合，对应最小项0、2、5、7、8、10。

在卡诺图中标注最小项

将上述最小项标注在卡诺图网格中。每个单元格对应特定最小项编号，在0、2、5、7、8、10号单元格标记1，其余保持0。

在卡诺图中标注最小项

分组技巧：大小、形状与位置

标注完成后，对1进行分组以简化逻辑表达式。我们聚焦三个要素：分组大小、形状与布局策略。

大小：尽可能最大化

分组应尽可能大（1、2、4或8单元格）。例如4单元格组比2单元格组更高效。目标是用最少组数覆盖所有1。

形状：保持矩形结构

分组必须形成矩形（行、列或2×2块状）。L型或锯齿状不符合规范，矩形结构能确保逻辑简洁性。

布局：智能利用网格特性

分组可跨越边界、环绕边缘或适当重叠。这种策略能实现高效覆盖，使简化过程清晰直观。

2单元格组

4单元格组

处理边界情况与环绕分组

某些1看似分散，实则通过网格环绕特性相连。以下示例展示如何利用该特性进行分组。

边缘连接原理

若顶部与底部行均有1，看似分离实则通过垂直环绕形成连续组。左右边缘同理，可通过水平环绕连接。

四角联动现象

四个角落的1通过双向环绕形成四单元格组。这种特性极大扩展了分组可能性。

水平环绕组

边界环绕组

解析分组生成乘积项

将每个分组转化为包含A、B、C、D的乘积项。观察组内保持不变的变量，变化变量则被省略。以下展示2、4、8单元格组的转化实例。

2单元格组解析

以相邻两单元格组为例：表达式AB'C'D + AB'CD中，A保持1，B保持0，D保持1，C在0/1间变化。省略C后得到简化项AB'D。

2单元格组示意图

2单元格组简化结果

4单元格组解析

以2×2区块为例：表达式A'BC'D + A'BCD + ABC'D + ABCD中，B保持1，D保持1，A与C变化。省略A、C后得到简化项BD。

4单元格组示意图

4单元格组简化结果

8单元格组解析

以占据半图的八单元格组为例：当A保持0，B、C、D全组合变化时，仅保留A'。更大分组意味着更简表达式。

8单元格组示意图

8单元格组简化结果

简化原理剖析

分组通过合并输入组合实现简化。组内变化的变量不影响结果模式，因此被省略。每个乘积项（如AB'D或A'）都是最终表达式的核心组件。

构建最终SOP表达式

将所有乘积项用加号连接，形成积之和（SOP）表达式。例如分组得到AB'D、AD'和A'时，最终表达式为A' + AB'D + AD'。

重叠分组的应用场景

当单个1可归属多个分组时，采用重叠策略能进一步优化。这在单元格无法完美匹配单一分组，或共享可减少总项数时特别有效。

例如第2行第3列的1可同时属于四单元格行组与两单元格列组。这种重叠能显著简化最终表达式。

重叠分组示意图

卡诺图简化流程概要

四变量卡诺图简化如同解谜：建立网格并标注布尔表达式的1，将其分组成尽可能大的矩形区块（可环绕边缘）。每个区块转化为简洁项，最终组合为最简SOP表达式。这种可视化方法是处理数字逻辑的高效方案。

进阶学习资源

通过可视化卡诺图求解器进行交互式练习，深入掌握简化技巧。尝试我们的 卡诺图求解器 来实验您自己的布尔表达式。