Introdução
O que é um Mapa de Karnaugh?
Você já se perguntou como os computadores tomam decisões? Eles usam algo chamado lógica booleana, que trabalha com valores verdadeiros e falsos. Essas declarações podem ficar bem complexas quando combinadas. É aqui que o Mapa de Karnaugh, ou K-Map, entra em ação. Um K-Map é uma ferramenta visual que organiza essas expressões lógicas em uma grade. Essa grade mostra todas as combinações possíveis de variáveis, permitindo identificar padrões rapidamente. Identificar esses padrões ajuda a simplificar a lógica.
Para aprofundar-se no que é um K-Map ou como resolver um K-Map de 4 variáveis, confira o artigo de referência: How to Solve a 4-Variable K-Map
Por que usar um K-Map de cinco variáveis?
A maioria dos K-Maps lida com duas, três ou quatro variáveis. Mas às vezes enfrentamos desafios maiores com cinco variáveis. Imagine projetar um circuito com cinco interruptores - cada um pode estar ligado ou desligado. São muitas combinações! Um K-Map de cinco variáveis ajuda a gerenciar essa complexidade, simplificando expressões que seriam difíceis de resolver. Seja criando um dispositivo ou programando, esse método pode economizar tempo e esforço.
Entendendo a estrutura do K-Map de cinco variáveis
Layout e Atribuição de Variáveis
Um K-Map de cinco variáveis parece complexo, mas é uma extensão do que você já conhece. Visualize um K-Map de quatro variáveis: uma grade 4x4 com 16 células. Cada célula representa combinações de quatro variáveis como B,C,D,E. As linhas usam B e C, as colunas D e E. Agora adicione uma quinta variável, A. Para acomodar 32 combinações (2⁵ = 32), usamos duas grades 4x4 lado a lado. Uma grade representa A=0 e outra A=1. Em cada grade, linhas mantêm B e C, colunas D e E - mantendo a familiaridade com a variável extra.

Diferenças em relação aos K-Maps de quatro variáveis
Principais diferenças do K-Map de cinco variáveis:
- Mais células: 32 células ao invés de 16 devido à quinta variável
- Estrutura dupla: Duas grades para A=0 e A=1
- Adjacência entre grades: Células em posições equivalentes nas duas grades são vizinhas
- Grupos maiores: Podem abranger até 32 células
A ideia básica de agrupamento permanece a mesma.
Como construir um K-Map de cinco variáveis
Passo 1: Determinar as Variáveis
Comece com cinco variáveis (A,B,C,D,E). Sua tarefa é determinar quando a função booleana é verdadeira (1) ou falsa (0) para todas combinações.
Passo 2: Rotular Linhas e Colunas
Use código Gray para linhas (B,C) e colunas (D,E): 00, 01, 11, 10. A grade esquerda representa A=0, a direita A=1.
Passo 3: Preencher os Valores
Para cada combinação A,B,C,D,E, insira 1 ou 0. Use a grade esquerda para A=0 e direita para A=1. Minterms (combinações onde a função é 1) devem ser preenchidos com 1s.
Como Agrupar Células em um K-Map de Cinco Variáveis
Regras de Agrupamento
Simplificação ocorre agrupando 1s seguindo estas regras:
- Grupos devem ter tamanho potência de dois: 1,2,4,8,16 ou 32
- Formato quadrado ou retangular (ex: 2x2 ou 1x4)
- Todas células do grupo devem ser adjacentes
- Crie os maiores grupos possíveis
- Cada 1 deve estar em pelo menos um grupo

Identificando Células Adjacentes
Células são adjacentes se diferirem em apenas uma variável. Na mesma grade, vizinhas horizontal/vertical. Entre grades, mesma posição em A=0 e A=1 são vizinhas (mudando apenas A).
Lidando com Continuidade de Bordas
Em K-Maps, as bordas se conectam: topo com fundo, esquerda com direita. Grupos podem cruzar as grades se estiverem na mesma posição, como se o mapa dobrasse.

Simplificando Expressões Booleanas com K-Map de Cinco Variáveis
Encontrando Implicantes Primos
Implicante primo é um grupo máximo de 1s que não pode ser expandido. Identifique todos grupos possíveis seguindo as regras.
Selecionando Implicantes Primos Essenciais
Implicantes essenciais cobrem 1s que só pertencem a um grupo. Inclua esses primeiro. Para 1s restantes, escolha grupos que cubram mais termos com menos grupos.
Escrevendo a Expressão Mínima
Cada grupo gera um termo:
- Identifique variáveis constantes no grupo
- Inclua variáveis sempre 1 (ex: B)
- Inclua negação se sempre 0 (ex: B')
- Ignore variáveis que mudam
A expressão final é a OR dos termos dos grupos selecionados.

Exemplos de Simplificação com K-Map de Cinco Variáveis
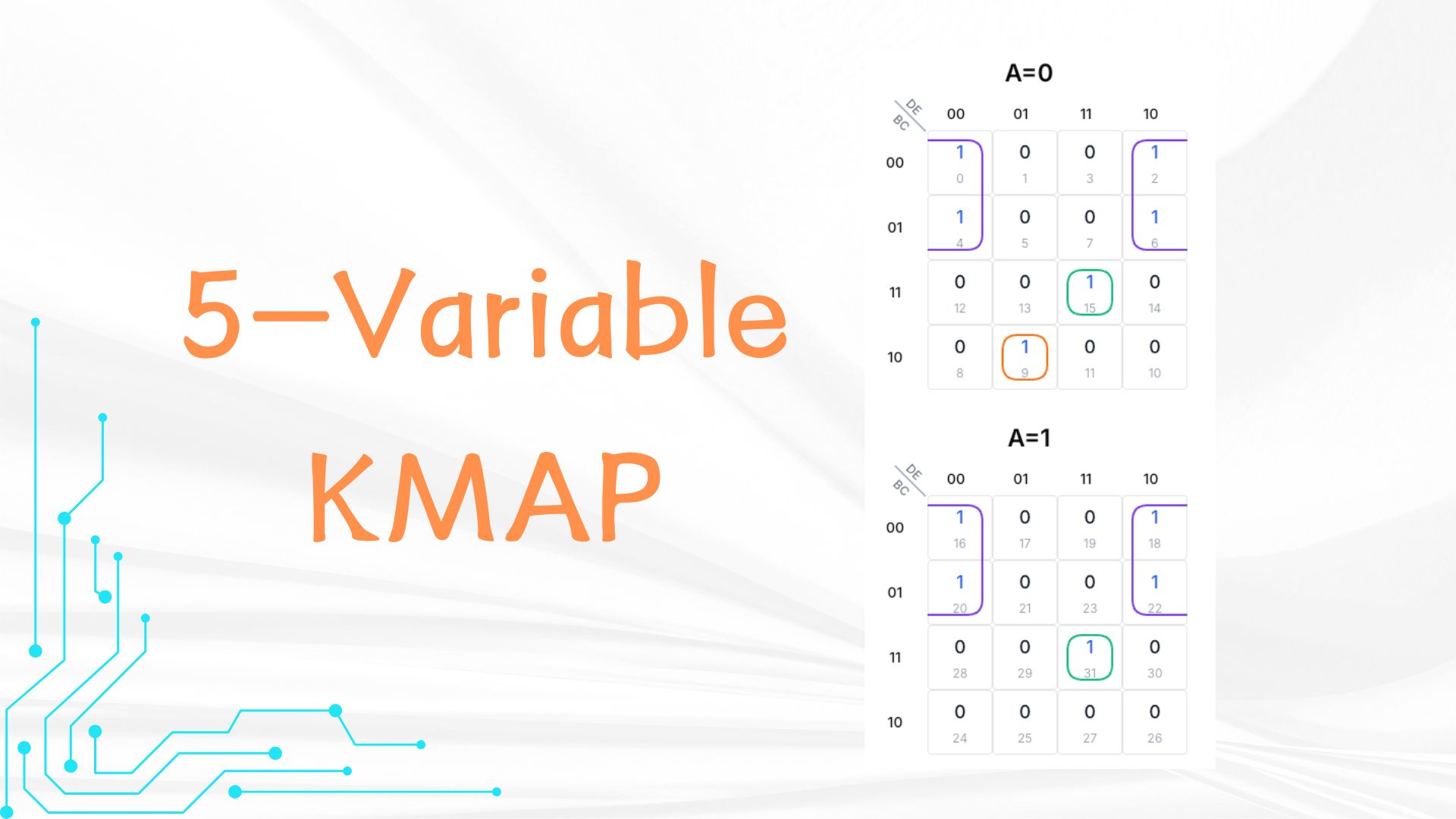
Considere a expressão: A'B'C'D'E' + A'B'C'DE' + A'B'CD'E' + A'B'CDE' + A'BC'D'E + A'BCDE + AB'C'D'E' + AB'C'DE' + AB'CD'E' + AB'CDE' + ABCDE. Em binário: células 0,2,4,6,9,15,16,18,20,22,31.
Passo 1: Preencher o K-Map
Na grade A=0 (B,C nas linhas; D,E nas colunas):
- Linha 00, coluna 00: 1
- Linha 00, coluna 01: 1
- Linha 01, coluna 11: 1
- Linha 01, coluna 10: 1
- Linha 11, coluna 11: 1
- Linha 10, coluna 01: 1
In the A=1 grid, rows are also B and C (00, 01, 11, 10), columns are also D and E (00, 01, 11, 10). Put 1s:
- Linha 00, coluna 00: 1
- Linha 00, coluna 01: 1
- Linha 01, coluna 11: 1
- Linha 01, coluna 10: 1
- Linha 11, coluna 11: 1

Passo 2: Agrupar os 1s
11 células com 1: 6 em A=0, 5 em A=1.
- Grupo 1: Termo único A'BC'D'E
- Grupo 2: 8 termos com B' e E' constantes
- Grupo 3: A'BCDE + ABCDE

Passo 3: Simplificar
- Grupo 1: Mantém A'BC'D'E
- Grupo 2: Simplifica para B'E'
- Grupo 3: Simplifica para BCDE
Expressão simplificada: A'BC'D'E + B'E' + BCDE

Dicas para Dominar K-Maps de Cinco Variáveis
Erros Comuns a Evitar
- Rotulação errada: Não usar código Gray
- Esquecer conexões entre grades
- Agrupar células não adjacentes
- Grupos pequenos demais
- Termos incorretos por variáveis mutáveis
Melhores Práticas para Eficiência
- Sempre use código Gray
- Priorize grupos grandes
- Verifique pares entre grades A=0 e A=1
- Garanta cobertura total dos 1s
- Valide termos com a grade
Pratique com nosso interactive K-Map Solver Tool que suporta até 5 variáveis. É ótimo para verificar soluções e ganhar confiança.