Como resolver um K-Map de 4 variáveis: Um guia claro e prático

O que é um K-Map e seu papel na lógica digital

K-Map, abreviação de Mapa de Karnaugh, ajuda a simplificar expressões booleanas na lógica digital. Essas expressões funcionam como instruções para circuitos digitais, usando valores verdadeiros e falsos para transformar entradas em saídas. Simplificá-las torna os circuitos menores, mais rápidos e mais baratos de construir.

O K-Map usa uma grade de quadrados para isso. Em um mapa de 4 variáveis, há 16 quadrados. Cada quadrado representa uma combinação única de quatro entradas. Os quadrados adjacentes diferem em apenas uma variável. Essa estrutura nos permite identificar padrões e agrupar saídas similares para simplificar a expressão.

A vantagem dos K-Maps está na visualização intuitiva. Eles superam métodos matemáticos puros ao reduzir erros. São mais eficazes com quatro ou cinco variáveis, atendendo à maioria dos projetos de circuitos reais.

Entendendo a Grade e Atribuição de Variáveis

Um K-Map de 4 variáveis começa com uma grade 4×4. Ela possui 16 quadrados, um para cada combinação possível de quatro entradas: A, B, C e D. Rotulamos as linhas com pares de A e B nas laterais. As colunas recebem pares de C e D no topo. Preenchemos cada quadrado com 1 ou 0, dependendo do problema lógico, transformando-o em uma imagem simplificável.

Grade do K-Map de 4 Variáveis com Números das Células (Mintermos)

Importância do Código Gray nos K-Maps

Observe um K-Map de 4 variáveis. Os rótulos das linhas e colunas não seguem a sequência 00, 01, 10, 11. Eles usam o código Gray: 00, 01, 11, 10. Isso não é aleatório. O código Gray muda apenas um bit por vez. Por exemplo, de 01 para 11, apenas o primeiro bit alterna.

Isso é crucial. Cada quadrado no K-Map representa uma combinação de variáveis. Quadrados vizinhos diferem por apenas uma variável, graças ao código Gray. Isso facilita o agrupamento durante a simplificação. Sem o código Gray, os quadrados não se alinhariam corretamente, complicando o agrupamento.

Convertendo a Função Booleana para Mintermos

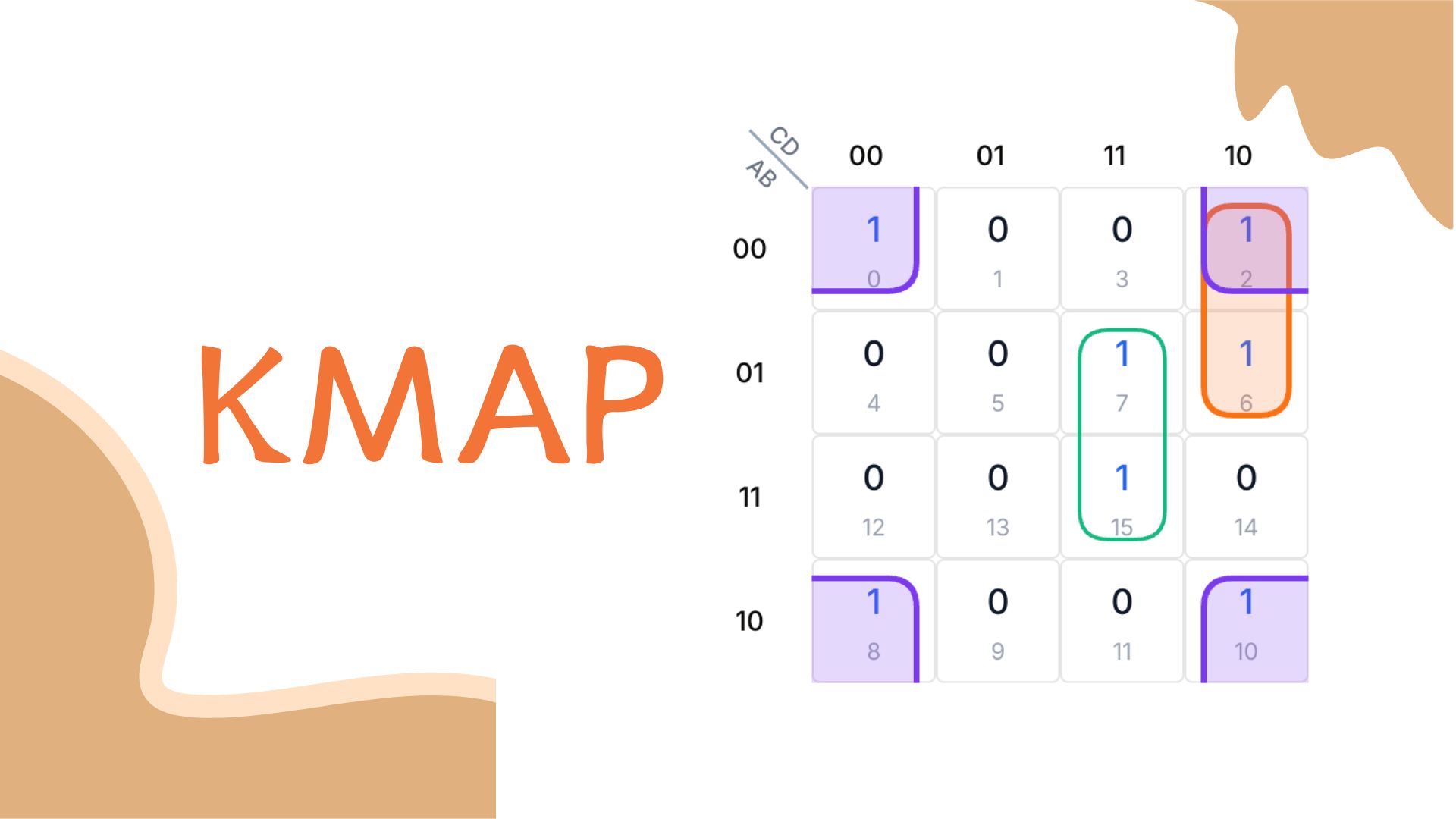
Para usar um K-Map de 4 variáveis, primeiro identificamos as combinações de entrada que tornam a função booleana verdadeira. Chamamos essas de mintermos. Exemplo: F = A'B'C'D' + A'B'CD' + A'BC'D + A'BCD + AB'C'D' + AB'CD'. Cada parte representa uma combinação de A, B, C e D que resulta em 1. Essas correspondem aos mintermos 0, 2, 5, 7, 8 e 10.

Plotando Mintermos no K-Map

Em seguida, posicionamos esses mintermos na grade do K-Map. Cada quadrado está vinculado a um número de mintermo. Marcamos 1 nos quadrados correspondentes aos mintermos 0, 2, 5, 7, 8 e 10. Os demais permanecem 0.

Plotando Mintermos no K-Map

Técnicas de Agrupamento: Tamanho, Formato e Posição

Após plotar os mintermos, agrupamos os 1s no K-Map. O agrupamento simplifica a expressão lógica. Focamos em três aspectos: tamanho, formato e posição. Vejamos cada um.

Tamanho: Priorize Grupos Grandes

Criamos grupos tão grandes quanto possível. Um grupo pode ter 1, 2, 4 ou 8 quadrados. Grupos maiores simplificam mais. Exemplo: um grupo de 4 é melhor que um de 2. Cobrimos todos os 1s com o menor número de grupos.

Formato: Use Retângulos

Grupos devem formar retângulos. Podem ser linhas, colunas ou blocos 2x2. Formatos como 'L' ou zigue-zague não funcionam. Retângulos mantêm a lógica simples e seguem as regras do K-Map.

Posição: Otimize o Uso da Grade

Posicionamos grupos para cobrir o máximo de 1s eficientemente. Grupos podem estar nas bordas, envolver a grade ou se sobrepor, se útil. Isso torna a simplificação clara.

Grupo de 2

Grupo de 4

Tratando Casos Especiais e Grupos que Envolvem a Grade

Alguns 1s parecem distantes, mas a grade é circular - as bordas opostas se conectam. Isso permite agrupar 1s aparentemente separados. Veja exemplos:

Bordas que se Conectam

Imagine 1s na linha superior e inferior. Eles parecem separados, mas o K-Map conecta topo e base, formando um grupo único. O mesmo vale para bordas laterais.

Cantos que se Ligam

1s nos quatro cantos (superior-esquerdo, superior-direito, inferior-esquerdo, inferior-direito) parecem dispersos. Mas o K-Map envolve ambas as direções, unindo-os em um grupo de quatro.

Grupo Horizontal

Grupo de Borda

Interpretando Grupos para Formar Termos Produto

Após agrupar os 1s, transformamos cada grupo em um termo produto usando A, B, C e D. Observamos o que permanece constante no grupo. Variáveis que mudam são omitidas, simplificando o termo. Veja exemplos para grupos de 2, 4 e 8.

Grupo de 2 Quadrados

Exemplo: AB'C'D + AB'CD. A=1, B=0, D=1 permanecem; C varia. Omitimos C. O termo simplificado é AB'D.

Grupo de 2 Quadrados

Grupo de 2 Simplificado

Grupo de 4 Quadrados

Exemplo: A'BC'D + A'BCD + ABC'D + ABCD. B=1, D=1 permanecem; A e C variam. Omitimos ambos. O termo simplificado é BD.

Grupo de 4 Quadrados

Grupo de 4 Simplificado

Grupo de 8 Quadrados

Exemplo: 8 quadrados com A=0 constante. B, C e D variam. O termo é A'. Grupos maiores resultam em termos mais curtos.

Grupo de 8 Quadrados

Grupo de 8 Simplificado

Por que a Simplificação Funciona

O agrupamento simplifica ao combinar combinações de entrada. Variáveis que mudam não afetam o padrão - são omitidas. Cada termo, como AB'D ou A', é uma parte essencial do resultado final.

Construindo a Expressão SOP Final

Combinamos todos os termos produto com sinais de adição, formando uma expressão SOP (Soma de Produtos). Exemplo: A' + AB'D + AD' é o resultado simplificado.

Quando Considerar Grupos Sobrepostos

Às vezes, um 1 pertence a múltiplos grupos (sobreposição). Isso ajuda a simplificar ainda mais. Use quando um 1 não se encaixa bem em um grupo único ou quando compartilhá-lo reduz o número de termos.

Exemplo: um quadrado na linha 2, coluna 3 participa de um grupo horizontal de 4 e um grupo vertical de 2. A sobreposição pode simplificar a expressão final.

Grupo Sobreposto

Resumo do Processo de Simplificação com K-Map

Simplificar com um K-Map de 4 variáveis é como resolver um quebra-cabeça. Configuramos a grade, plotamos os 1s da expressão booleana e agrupamos em retângulos de 1, 2, 4 ou 8 quadrados. Priorizamos grupos grandes que podem envolver bordas ou cantos, graças ao código Gray. Cada grupo vira um termo simples. Menos termos significam resultados mais enxutos. Cobrimos todos os 1s com o mínimo de grupos e escrevemos a expressão final - uma abordagem visual clara para a lógica digital.

Recursos para prática adicional

Pratique com solucionadores interativos de Mapas de Karnaugh que visualizam o processo de simplificação. Experimente nosso Solucionador de Mapas de Karnaugh para experimentar com suas próprias expressões booleanas.