KMap SolverKMap Solver

5変数K-Mapの解法：段階的な簡略化ガイド

このステップバイステップガイドで5変数K-Mapの解法をマスター。2つのグリッドをまたがる最小項のグループ化手法と複雑な論理式の簡略化方法を詳解します。

YiliaMarch 20, 2025
5変数K-Mapの解法：段階的な簡略化ガイド

はじめに

カルノー図（K-Map）とは？

コンピュータがどのように判断を下すか考えたことはありますか？それらは真偽値を扱うブール論理を使用しています。これらの真偽値を組み合わせると複雑になることがあります。そこで登場するのがカルノー図（K-Map）です。K-Mapは論理式を整然としたグリッドに配置する便利なツールです。このグリッドは全ての変数の組み合わせを視覚化し、パターンを素早く見つけられるようにします。これらのパターンを特定することで、論理式を簡略化することが可能になります。

K-Mapの詳細や4変数K-Mapの解法についてさらに学びたい方は、参考記事をご覧ください: 4変数K-Mapの解き方

5変数K-Mapが必要な理由

通常のK-Mapは2～4変数を扱いますが、5つの変数を持つ複雑な問題に直面することもあります。5つのスイッチを持つ回路を設計する場合、各スイッチのON/OFF状態の組み合わせは膨大になります。5変数K-Mapはこのような複雑さを管理し、通常では処理が困難な式を簡略化します。デバイスの設計やプログラミングにおいて、時間と労力を大幅に節約できるツールです。

5変数K-Mapの構造理解

レイアウトと変数割り当て

5変数K-Mapは4変数K-Mapの拡張です。4変数K-MapがB,C,D,Eの16組み合わせ（4x4グリッド）を表すのに対し、5変数ではAを追加し、2つの4x4グリッド（A=0とA=1）を使用します。各行はBとC、各列はDとEをグレイコード順（00,01,11,10）に配置します。これにより32通りの組み合わせ（2⁵=32）を扱いながら、既存の構造を維持できます。

5変数K-Map構造図
2つの4x4グリッドで構成される5変数K-Mapの基本構造

4変数K-Mapとの相違点

5変数K-Mapの主な特徴:

  • セル数増加：5番目の変数により32セルに拡張
  • 二重グリッド構造：A=0とA=1用の2グリッドを並列配置
  • グリッド間隣接：A=0グリッドのセルはA=1グリッドの同位置セルと隣接
  • 大規模グループ：最大32セルまでのグループ化が可能

基本的なグループ化の概念は4変数K-Mapと同じです

5変数K-Mapの作成方法

ステップ1: 変数の決定

A,B,C,D,Eの5変数を定義します。これらは回路のスイッチなど任意の要素を表せます。全ての組み合わせにおいてブール関数が真(1)か偽(0)かを判定します。

ステップ2: 行と列のラベル付け

2つの4x4グリッドを準備します。行（B,C）と列（D,E）にグレイコード（00,01,11,10）を適用し、左グリッドをA=0、右をA=1とマークします。これで準備完了です。

ステップ3: セルへの値入力

各A,B,C,D,Eの組み合わせに対し、関数値（1/0）を入力します。A=0は左グリッド、A=1は右グリッドに配置します。mintermリストがある場合、該当セルに1を入力します。

5変数K-Mapのグループ化手法

グループ化ルール

1のセルをグループ化して簡略化します:

  • グループサイズは2の累乗（1,2,4,8,16,32）
  • 正方形/長方形の形状を維持
  • 隣接セルのみグループ化（後述）
  • 可能な限り最大のグループを形成
  • 全ての1を最低1つのグループに包含
K-Mapグループ化ルール
5変数K-Mapにおける有効なグループ化例

隣接セルの特定

1変数のみが異なるセルは隣接とみなします。各グリッド内の水平/垂直隣接に加え、A=0とA=1グリッドの同位置セルも隣接です。例えばA=0グリッドの(00,00)セルはA=1グリッドの(00,00)セルと隣接し、グリッドを跨ぐグループ形成が可能です。

5変数における折り返し処理

K-Mapの端は反対側と接続されます。各グリッドで上端⇄下端、左端⇄右端が隣接し、さらにグリッド間でも同位置セルが接続されます。これにより複雑なグループ形成が可能になります。

K-Map折り返しグループ化
同じ色枠のセルが同一グループに属する例

5変数K-Mapを使った論理式簡略化

主項（Prime Implicant）の特定

主項とは拡張不可能な最大グループです。全ての可能なグループを検討し、これ以上結合できないグループを主項として特定します。これが簡略化式の基礎となります。

必須主項の選択

1つのグループにしか属さない1を含む主項は必須です。まず必須グループを選択し、残りの1をカバーする追加グループを選択します。効率的なカバレッジを心掛けます。

最簡形の作成

各グループから論理項を導出:

  • グループ内で不変の変数を特定
  • 常に1の変数はそのまま採用（例:B）
  • 常に0の変数は否定形を採用（例:B'）
  • 変化する変数は除外

各項をANDで結合し、全ての項をORで結合して最終式を完成させます。

K-Map解法例
5変数K-Mapからの簡略化例

5変数K-Map簡略化事例

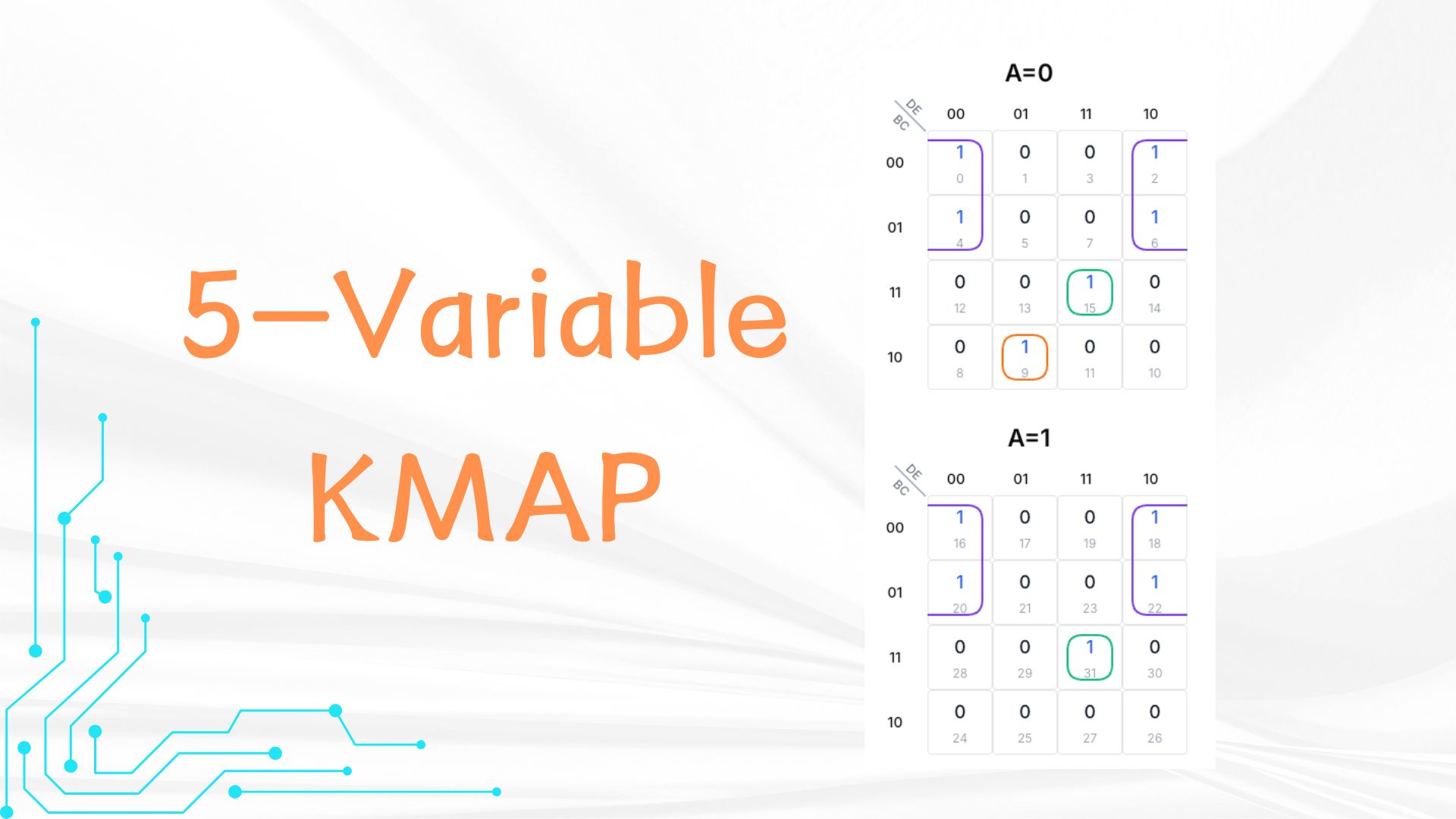
例: A'B'C'D'E' + ... + ABCDE（計11項）。2進数表現ではセル0,2,4,6,9,15,16,18,20,22,31に対応。

ステップ1: K-Mapへの入力

A=0グリッド（B,C行、D,E列）に1を配置:

  • 行00（B=0,C=0）列00（D=0,E=0）: 1
  • 行00（B=0,C=0）列01（D=1,E=0）: 1
  • 行01（B=0,C=1）列11（D=0,E=0）: 1
  • 行01（B=0,C=1）列10（D=1,E=0）: 1
  • 行11（B=1,C=1）列11（D=1,E=1）: 1
  • 行10（B=1,C=0）列01（D=0,E=1）: 1

In the A=1 grid, rows are also B and C (00, 01, 11, 10), columns are also D and E (00, 01, 11, 10). Put 1s:

  • 行00（B=0,C=0）列00（D=0,E=0）: 1
  • 行00（B=0,C=0）列01（D=1,E=0）: 1
  • 行01（B=0,C=1）列11（D=0,E=0）: 1
  • 行01（B=0,C=1）列10（D=1,E=0）: 1
  • 行11（B=1,C=1）列11（D=1,E=1）: 1
5変数K-Map入力例
K-Mapへの入力結果

ステップ2: 1のグループ化

A=0グリッドに6個、A=1グリッドに5個の1を配置:

  • グループ1: 単一項 A'BC'D'E
  • グループ2: 8項のB'E'グループ
  • グループ3: 2項のBCDEグループ
K-Mapグループ化例
グループ化結果

ステップ3: 式の簡略化

  • グループ1: A'BC'D'E を維持
  • グループ2: B'とE'が不変 → B'E'
  • グループ3: Aが変化 → BCDE

簡略化結果: A'BC'D'E + B'E' + BCDE

K-Map簡略化結果
最終的な簡略化式

5変数K-Map習得のコツ

よくある間違い

  • ラベル誤り: グレイコード未使用による隣接関係の崩れ
  • 接続見落とし: グリッド間接続の無視
  • 不適切グループ: 非隣接セルの包含
  • 過小グループ: 最大グループの見逃し
  • 項の誤生成: 不変変数の見誤り

効率的な手法

  • 行/列ラベルに必ずグレイコードを適用
  • 大規模グループから優先的に処理
  • グリッド間接続を積極的に活用
  • 1のカバレッジを常に確認
  • 結果をグリッドで再確認

これらの手法を習得したら、当サイトの 対話型K-Mapソルバー で実践練習をしてみましょう。5変数まで対応したツールで、理解を深めながら自信をつけることができます。