4変数K-Mapの解き方：わかりやすく実践的なガイド

K-Mapとは？デジタル論理回路における役割

K-Map（カルノー図）はデジタル論理回路におけるブール式の簡略化を支援します。これらの式はデジタル回路の指令書のような役割を果たし、真偽値を使って入力を出力に変換します。式を簡略化することで、回路をより小型化・高速化し、コスト削減を実現します。

K-Mapは格子状の正方形を使用します。4変数マップの場合16個のセルで構成され、各セルは4つの入力のユニークな組み合わせを表します。隣接するセルは1つの入力のみが異なるよう配置されており、パターン認識とグループ化による式の簡略化を可能にします。

K-Mapの強みは視覚的で直感的な操作にあります。数学的手法よりもミスを減らし、4～5変数の現実的な回路設計に最適化されています。

グリッド構造と変数割り当ての理解

4変数K-Mapは4×4グリッド（16セル）から構成されます。行にAとBの組み合わせ、列にCとDの組み合わせを配置し、各セルに論理問題に応じた1/0を記入します。これにより問題を視覚的に簡略化可能な状態に変換します。

4変数K-Mapグリッドとセル番号（minterm）

K-Mapにおけるグレイコードの重要性

K-Mapの行/列ラベルは通常の二進数（00,01,10,11）ではなく、グレイコード（00,01,11,10）を使用します。グレイコードは1ビットのみ変化する特性を持ち、隣接セル間の変数変化を最小限に抑えます。

この特性により、隣接セルが1変数のみ異なる状態を維持し、グループ化による簡略化を容易にします。グレイコードなしでは適切なグループ形成が困難になります。

ブール関数からmintermへの変換

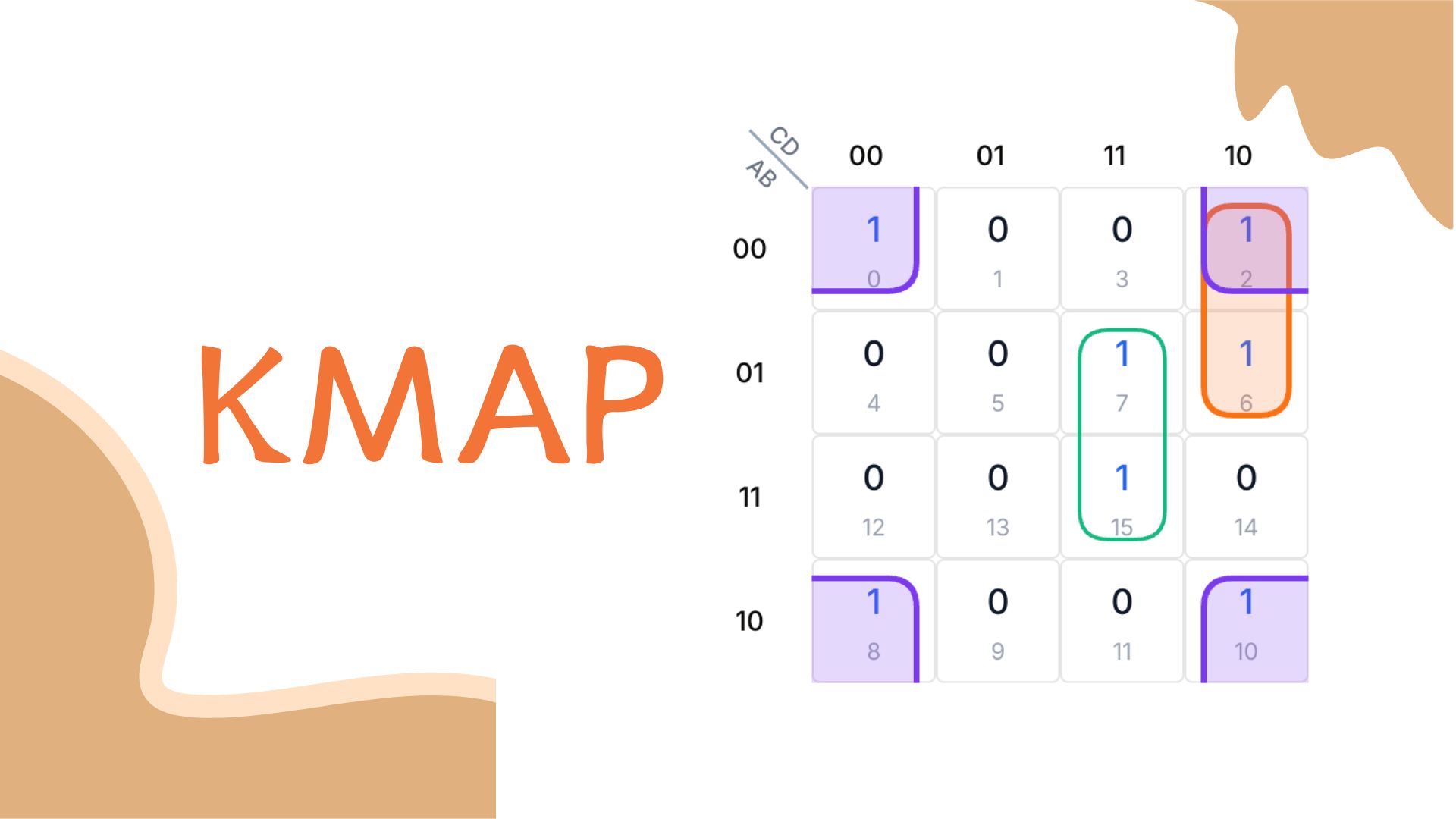
4変数K-Map使用時には、まずブール関数が真となる入力組み合わせ（minterm）を特定します。例：F = A'B'C'D' + A'B'CD' + A'BC'D + A'BCD + AB'C'D' + AB'CD'の場合、minterm 0,2,5,7,8,10が該当します。

K-Mapへのmintermプロット

特定したminterm番号に対応するセルに1を記入します。その他のセルは0のまま維持します。

K-Mapへのmintermプロット

グループ化技法：サイズ・形状・配置

1のセルをグループ化する際は、サイズ（可能な限り大規模）、形状（矩形限定）、配置（効率的なカバレッジ）の3要素を最適化します。

サイズ：最大グループを優先

1,2,4,8セルのグループを形成可能。大規模グループほど簡略化効果が高く、最小数のグループで全1をカバーすることを目指します。

形状：矩形に限定

行・列・ブロック（2x2等）の矩形形状のみ有効。L字やジグザグ形状は不可です。

配置：グリッド特性を活用

端間の接続・重複を活用し効率的に1をカバーします。上下端・左右端の接続特性を最大限活用します。

2セルグループ

4セルグループ

エッジケースとラップアラウンド処理

一見離れたセルもグリッドの接続特性を活用してグループ化可能です。具体的な処理例を以下に示します。

端の接続

上下端・左右端が接続されている特性を活用し、見かけ上離れたセルを1グループに統合します。

コーナーの接続

四隅のセルも双方向のラップアラウンド特性により、4セルグループとして統合可能です。

水平グループ

エッジグループ

グループ解釈と積項の形成

各グループから積項を生成します。グループ内で変化しない変数のみを保持し、変化する変数を除外することで簡略化を実現します。

2セルグループの例

隣接2セルの場合、変化しない変数のみを保持（例：AB'D）し、変化変数（C）を除外します。

2セルグループ

簡略化後

4セルグループの例

2x2ブロックの場合、2変数が変化するため保持変数を更に削減（例：BD）します。

4セルグループ

簡略化後

8セルグループの例

8セルグループの場合、3変数が変化するため単一変数（例：A'）のみを保持します。

8セルグループ

簡略化後

簡略化の原理

グループ化により入力組み合わせを束ね、変化変数を除外することで論理式を本質的な部分のみに縮約します。

最終SOP式の構築

全積項を加算記号で結合し、SOP形式の簡略式を完成させます（例：A' + AB'D + AD'）。

重複グループの活用タイミング

1つのセルが複数グループに属する場合、項数を削減できる場合に重複を許可します。

例：行グループ（4セル）と列グループ（2セル）が交差するセルを共有し、全体の簡略化を最適化します。

重複グループ例

K-Map簡略化プロセスの概要

4変数K-Mapによる簡略化はパズル解法に似ています。グリッド設定→1のプロット→最大矩形グループ形成→積項導出→SOP式構築の流れで、視覚的に論理式を最適化します。

さらなる練習のためのリソース

簡略化プロセスを視覚化するインタラクティブなKマップソルバーで練習しましょう。私たちの Kマップソルバー を試して、あなた自身のブール式で実験してみてください。