Pengenalan
Apa itu Karnaugh Map?
Pernahkah Anda bertanya-tanya bagaimana komputer mengambil keputusan? Mereka menggunakan logika Boolean yang berhubungan dengan nilai benar dan salah. Pernyataan benar-salah ini bisa menjadi rumit ketika dikombinasikan. Di sinilah Karnaugh Map atau K-Map berperan. K-Map adalah alat sederhana yang mengorganisir pernyataan logika dalam grid rapi. Grid ini memetakan semua kombinasi variabel yang mungkin, memudahkan identifikasi pola. Pola ini membantu menyederhanakan logika.
Untuk mempelajari lebih dalam tentang K-Map atau cara menyelesaikan K-Map 4-variabel, baca artikel referensi: How to Solve a 4-Variable K-Map
Mengapa Menggunakan K-Map Lima Variabel?
K-Map umumnya menangani 2-4 variabel. Namun tantangan lebih besar muncul dengan 5 variabel. Bayangkan merancang sirkuit dengan 5 saklar - masing-masing bisa aktif/nonaktif. Kombinasi yang sangat banyak! K-Map 5-variabel membantu mengelola kompleksitas ini. Alat ini menyederhanakan ekspresi yang sulit diolah. Baik untuk membangun gadget atau pemrograman, K-Map 5-variabel menghemat waktu dan usaha.
Memahami Struktur K-Map Lima Variabel
Tata Letak dan Penempatan Variabel
K-Map 5-variabel adalah perluasan dari K-Map 4-variabel. Bayangkan grid 4x4 dengan 16 sel (mewakili kombinasi B,C,D,E). Baris menggunakan B dan C, kolom D dan E. Tambahkan variabel kelima A. Untuk 32 kombinasi (2⁵), gunakan dua grid 4x4 berdampingan. Grid kiri untuk A=0, kanan A=1. Tata letak baris dan kolom tetap sama, mempertahankan kemiripan struktur.

Perbedaan dari K-Map 4-Variabel
Perbedaan utama K-Map 5-variabel:
- Lebih Banyak Sel: 32 sel alih-alih 16 karena variabel kelima
- Struktur Grid Ganda: Dua grid untuk A=0 dan A=1
- Adjacency Lintas Grid: Sel bisa 'bertetangga' antar grid
- Grup Lebih Besar: Grup hingga 32 sel (umumnya lebih kecil)
Tenang—konsep pengelompokan tetap sama.
Cara Membuat K-Map Lima Variabel
Langkah 1: Tentukan Variabel
Mulai dengan 5 variabel (A,B,C,D,E). Tentukan kapan fungsi Boolean bernilai benar (1) atau salah (0) untuk semua kombinasi.
Langkah 2: Labeli Baris dan Kolom
Siapkan dua grid 4x4. Labeli baris dengan B dan C menggunakan Gray code: 00, 01, 11, 10. Kolom dengan D dan E juga Gray code. Grid kiri A=0, kanan A=1.
Langkah 3: Isi Sel dengan Nilai Fungsi
Isi setiap kombinasi A,B,C,D,E dengan 1 atau 0. Untuk A=0, gunakan grid kiri; A=1 grid kanan. Jika ada daftar minterms (kombinasi dengan fungsi=1), isi 1 di sel tersebut.
Cara Mengelompokkan Sel dalam K-Map 5-Variabel
Aturan Pengelompokan
Aturan penyederhanaan dengan pengelompokan 1:
- Ukuran grup harus pangkat dua: 1, 2, 4, 8, 16, atau 32
- Bentuk persegi/persegi panjang (2x2 atau 1x4)
- Semua sel dalam grup harus adjacent (bertetangga)
- Buat grup sebesar mungkin
- Setiap 1 harus masuk minimal satu grup

Mengidentifikasi Sel Tetangga
Sel disebut adjacent jika berbeda satu variabel. Dalam grid, sel horizontal/vertikal berdekatan adalah adjacent. Sel di grid A=0 adjacent dengan posisi sama di A=1. Contoh: sel row 00, column 00 (A=0) adjacent dengan row 00, column 00 (A=1).
Menangani Wrap-Around Lima Variabel
Edge K-Map bersambung: baris atas-bawah dan kolom kiri-kanan terhubung. Sel juga bisa terhubung antar grid A=0 dan A=1. Ini memungkinkan pengelompokan lintas grid di posisi sama.

Menyederhanakan Ekspresi Boolean dengan K-Map 5-Variabel
Mencari Prime Implicants
Prime implicant adalah grup 1 terbesar yang mungkin. Cari semua grup 1 sesuai aturan. Pastikan grup tidak bisa digabung lagi. Inilah building block ekspresi sederhana.
Memilih Essential Prime Implicants
Essential prime implicants adalah grup yang wajib ada. Cari 1 yang hanya masuk satu grup. Grup ini harus dimasukkan. Untuk 1 yang belum tercakup, pilih grup tambahan dengan cakupan terluas.
Menulis Ekspresi Minimal
Cara membuat term dari grup:
- Identifikasi variabel konstan dalam grup
- Variabel selalu 1: tulis sebagai B
- Variabel selalu 0: tulis sebagai B'
- Abaikan variabel yang berubah
Gabungkan term dengan AND, lalu OR-kan semua term. Hasilnya adalah ekspresi Boolean sederhana!

Contoh Penyederhanaan K-Map 5-Variabel
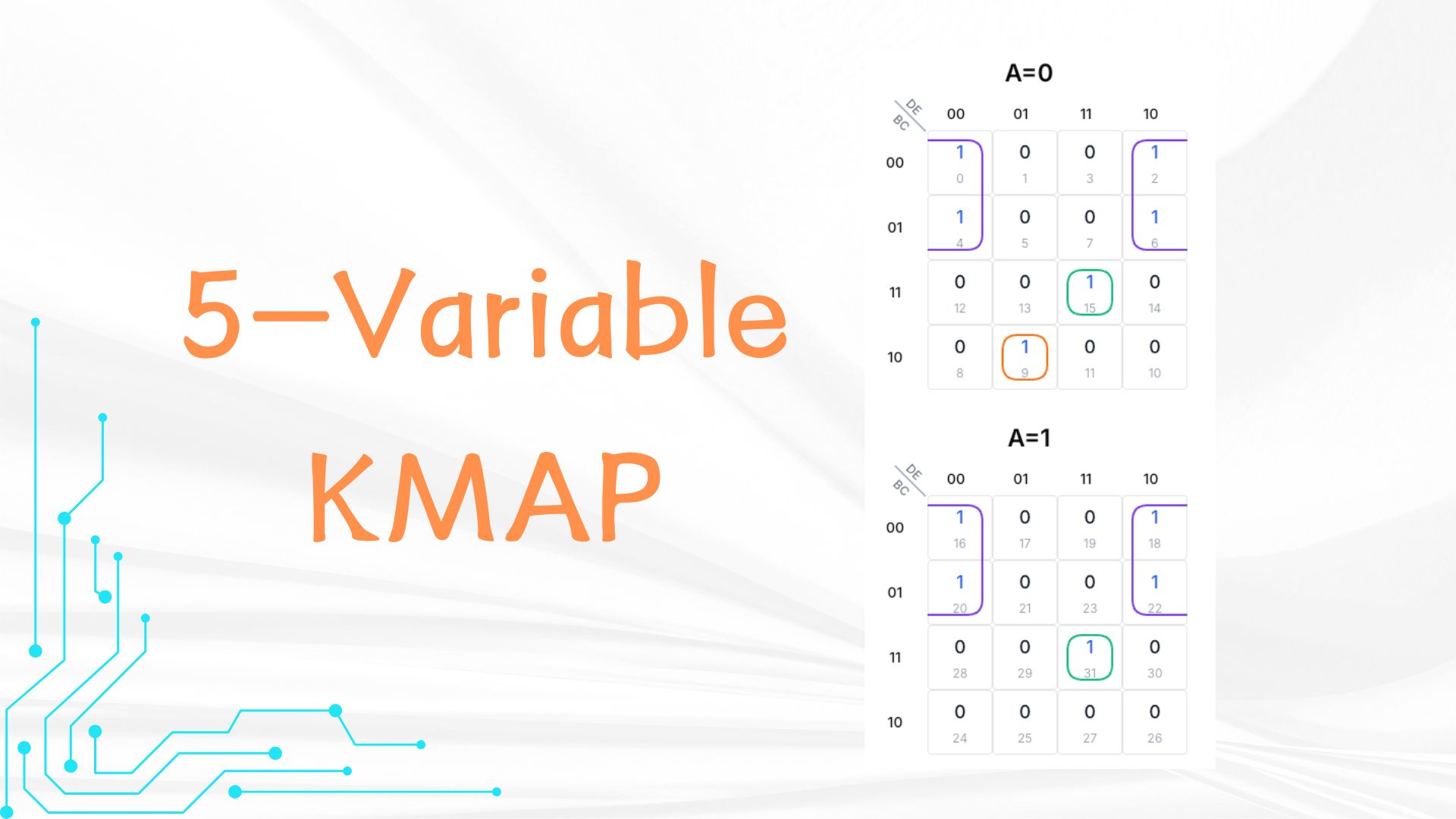
Contoh ekspresi Boolean: A'B'C'D'E' + A'B'C'DE' + A'B'CD'E' + A'B'CDE' + A'BC'D'E + A'BCDE + AB'C'D'E' + AB'C'DE' + AB'CD'E' + AB'CDE' + ABCDE. Dalam biner: sel 00000 (0), 00010 (2), 00100 (4), 00110 (6), 01001 (9), 01111 (15), 10000 (16), 10010 (18), 10100 (20), 10110 (22), 11111 (31).
Langkah 1: Isi K-Map
Di grid A=0 (B dan C sebagai baris, D dan E kolom):
- Baris 00 (B=0,C=0), kolom 00 (D=0,E=0): 1
- Baris 00 (B=0,C=0), kolom 01 (D=1,E=0): 1
- Baris 01 (B=0,C=1), kolom 11 (D=0,E=0): 1
- Baris 01 (B=0,C=1), kolom 10 (D=1,E=0): 1
- Baris 11 (B=1,C=1), kolom 11 (D=1,E=1): 1
- Baris 10 (B=1,C=0), kolom 01 (D=0,E=1): 1
In the A=1 grid, rows are also B and C (00, 01, 11, 10), columns are also D and E (00, 01, 11, 10). Put 1s:
- Baris 00 (B=0,C=0), kolom 00 (D=0,E=0): 1
- Baris 00 (B=0,C=0), kolom 01 (D=1,E=0): 1
- Baris 01 (B=0,C=1), kolom 11 (D=0,E=0): 1
- Baris 01 (B=0,C=1), kolom 10 (D=1,E=0): 1
- Baris 11 (B=1,C=1), kolom 11 (D=1,E=1): 1

Langkah 2: Kelompokkan 1
Ada 11 angka 1: 6 di grid A=0 dan 5 di A=1.
- Grup 1: Term tunggal: A'BC'D'E
- Grup 2: A'B'C'D'E' + A'B'C'DE' + A'B'CD'E' + A'B'CDE' + AB'C'D'E' + AB'C'DE' + AB'CD'E' + AB'CDE'
- Grup 3: A'BCDE + ABCDE

Langkah 3: Sederhanakan
- Grup 1: Pertahankan term tunggal: A'BC'D'E
- Grup 2: Hanya B' dan E' konstan → B'E'
- Grup 3: Hanya A yang berubah → BCDE
Ekspresi sederhana: A'BC'D'E + B'E' + BCDE

Tips Menguasai K-Map 5-Variabel
Kesalahan Umum yang Harus Dihindari
- Label Salah: Tidak menggunakan Gray code
- Lupa Koneksi Antar Grid
- Pengelompokan Tidak Valid
- Grup Terlalu Kecil
- Term Tidak Sesuai
Praktik Terbaik untuk Efisiensi
- Selalu gunakan Gray code
- Cari grup terbesar dulu
- Periksa kemungkinan grup lintas grid
- Pastikan semua 1 tercakup
- Verifikasi term dengan grid
Untuk mempraktikkan pengetahuan ini, coba interactive K-Map Solver Tool yang mendukung hingga 5 variabel. Alat ini membantu memverifikasi pekerjaan dan meningkatkan kepercayaan diri. Terus berlatih hingga semudah K-Map 4-variabel!