Cara Menyelesaikan K-Map 4 Variabel: Panduan Jelas dan Praktis

Apa itu K-Map dan Perannya dalam Logika Digital

K-Map, singkatan dari Karnaugh Map, membantu menyederhanakan ekspresi Boolean dalam logika digital. Ekspresi ini berfungsi seperti instruksi untuk sirkuit digital, menggunakan nilai benar dan salah untuk mengubah input menjadi output. Penyederhanaan membuat sirkuit lebih kecil, cepat, dan hemat biaya.

K-Map menggunakan grid kotak untuk tujuan ini. Dalam peta 4-variabel, terdapat 16 kotak. Setiap kotak merepresentasikan kombinasi unik dari empat input. Kotak-kotak berdekatan hanya berbeda satu variabel. Susunan ini memungkinkan identifikasi pola dan pengelompokan output serupa untuk menyederhanakan ekspresi.

K-Map unggul karena visual dan mudah digunakan. Metode ini mengungguli pendekatan matematis murni dengan mengurangi kesalahan. Optimal untuk 4-5 variabel, sesuai dengan kebanyakan desain sirkuit dunia nyata.

Memahami Grid dan Penempatan Variabel

K-Map 4-variabel dimulai dengan grid 4×4 berisi 16 kotak untuk setiap kombinasi input A, B, C, D. Baris diberi label pasangan A dan B di sisi, kolom dengan pasangan C dan D di atas. Setiap kotak diisi 1 atau 0 sesuai masalah logika, mengubah masalah menjadi representasi visual yang bisa disederhanakan.

Grid K-Map 4-Variabel dengan Nomor Sel (Minterm)

Pentingnya Kode Gray dalam K-Map

Perhatikan label baris dan kolom K-Map 4-variabel. Alih-alih 00, 01, 10, 11 seperti hitungan biner, digunakan kode Gray: 00, 01, 11, 10. Kode Gray hanya mengubah satu bit per langkah, misal dari 01 ke 11 hanya bit pertama yang berubah.

Ini krusial untuk pengelompokan. Setiap kotak merepresentasikan kombinasi variabel dimana kotak bertetangga hanya berbeda satu variabel berkat kode Gray. Tanpa kode Gray, pengelompokan menjadi sulit.

Mengkonversi Fungsi Boolean ke Minterm

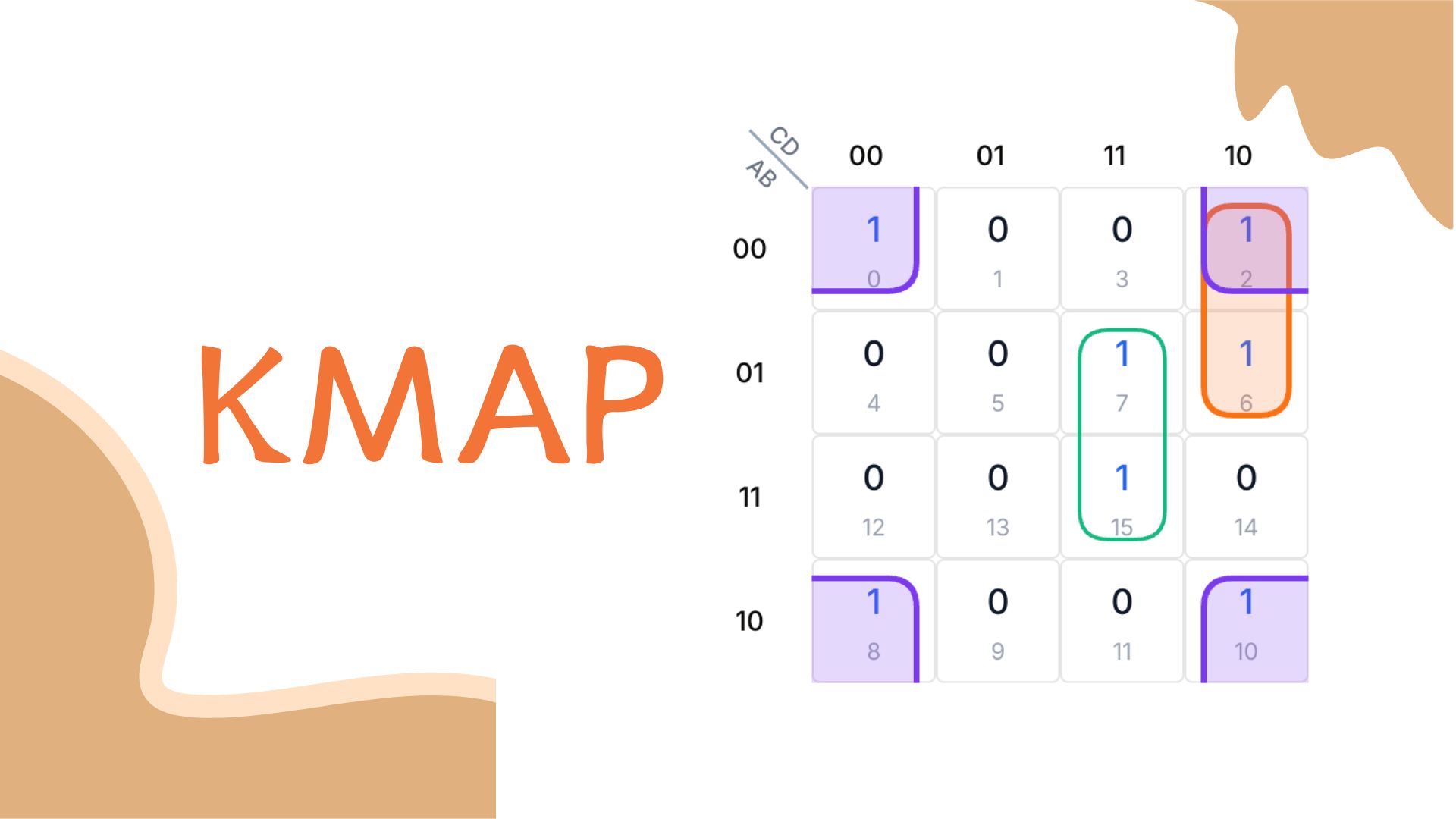
Untuk menggunakan K-Map 4-variabel, pertama tentukan kombinasi input yang membuat fungsi Boolean benar (minterm). Contoh fungsi F = A'B'C'D' + A'B'CD' + A'BC'D + A'BCD + AB'C'D' + AB'CD' memiliki minterm 0, 2, 5, 7, 8, dan 10.

Memetakan Minterm pada K-Map

Tandai kotak dengan minterm 0, 2, 5, 7, 8, dan 10 sebagai 1. Sisanya tetap 0.

Memetakan Minterm pada K-Map

Teknik Pengelompokan: Ukuran, Bentuk, dan Posisi

Setelah memetakan minterm, kelompokkan angka 1. Fokus pada tiga aspek: ukuran, bentuk, dan posisi kelompok.

Ukuran: Semakin Besar Semakin Baik

Buat kelompok sebesar mungkin (1, 2, 4, atau 8 kotak). Kelompok besar memberikan penyederhanaan lebih optimal.

Bentuk: Pertahankan Persegi Panjang

Kelompok harus berbentuk persegi panjang (baris, kolom, atau blok 2x2). Bentuk tidak beraturan tidak valid.

Posisi: Manfaatkan Grid Secara Efisien

Kelompok bisa berada di tepi, melingkar, atau tumpang tindih untuk cakupan maksimal.

Kelompok 2

Kelompok 4

Menangani Kasus Tepi dan Kelompok Melingkar

Beberapa angka 1 mungkin terlihat terpisah, namun grid bersifat melingkar. Contoh penerapan:

Tepi yang Terhubung

Angka 1 di baris atas dan bawah sebenarnya terhubung secara vertikal. Demikian juga tepi kiri-kanan.

Sudut yang Berhubungan

Empat sudut grid yang terisi 1 dapat dikelompokkan sebagai satu kesatuan.

Kelompok Horizontal

Kelompok Tepi

Menginterpretasi Kelompok Menjadi Product Term

Setiap kelompok diubah menjadi product term dengan mempertahankan variabel yang konsisten dan menghilangkan yang berubah.

Kelompok 2 Kotak

Contoh kelompok dua kotak horizontal: AB'D (variabel C dihilangkan karena berubah).

Kelompok 2 Kotak

Kelompok 2 Tersederhanakan

Kelompok 4 Kotak

Contoh blok 2x2: BD (variabel A dan C dihilangkan).

Kelompok 4 Kotak

Kelompok 4 Tersederhanakan

Kelompok 8 Kotak

Kelompok setengah peta menghasilkan term sederhana seperti A' (variabel lain berubah).

Kelompok 8 Kotak

Kelompok 8 Tersederhanakan

Mengapa Penyederhanaan Berhasil

Variabel yang berubah dalam kelompok tidak mempengaruhi hasil akhir sehingga bisa dieliminasi.

Menyusun Ekspresi SOP Final

Gabungkan semua product term dengan tanda +. Contoh: A' + AB'D + AD'.

Kapan Menggunakan Kelompok Tumpang Tindih

Overlapping digunakan ketika satu kotak bisa masuk ke beberapa kelompok untuk meminimalkan jumlah term.

Contoh: Sebuah kotak di baris 2 kolom 3 bisa menjadi bagian kelompok horizontal dan vertikal sekaligus.

Kelompok Tumpang Tindih

Ringkasan Proses Penyederhanaan K-Map

Penyederhanaan dengan K-Map 4-variabel seperti menyelesaikan puzzle: siapkan grid, plot minterm, kelompokkan 1's sebesar mungkin (termasuk melingkar), lalu konversi menjadi ekspresi sederhana.

Sumber Daya untuk Latihan Lebih Lanjut

Berlatihlah dengan pemecah K-Map interaktif yang memvisualisasikan proses penyederhanaan. Coba Pemecah K-Map kami untuk bereksperimen dengan ekspresi Boolean Anda sendiri.