Résolvez les K-Map à 5 variables : Votre guide étape par étape pour la simplification

Qu'est-ce qu'une carte de Karnaugh ?

Vous êtes-vous déjà demandé comment les ordinateurs prennent des décisions ? Ils utilisent une logique booléenne qui manipule des valeurs vraies et fausses. Ces états logiques peuvent devenir complexes lorsqu'on les combine. C'est là que la carte de Karnaugh (K-Map) intervient comme outil salvateur. Une K-Map est un instrument visuel qui organise ces expressions logiques dans une grille structurée. Cette disposition révèle toutes les combinaisons possibles de variables, permettant de détecter rapidement des motifs récurrents pour simplifier la logique.

Pour approfondir le fonctionnement des K-Map ou apprendre à résoudre une K-Map à 4 variables, consultez notre article de référence: Comment résoudre une carte de Karnaugh à 4 variables

Pourquoi utiliser une carte de Karnaugh à cinq variables ?

Les K-Map classiques gèrent 2 à 4 variables. Mais certains défis nécessitent 5 variables. Imaginez concevoir un circuit avec 5 interrupteurs - chaque combinaison on/off crée une complexité exponentielle. La K-Map à cinq variables permet de maîtriser cette complexité en simplifiant des expressions autrement ingérables. Que vous développiez un circuit électronique ou un programme, cet outil vous fera gagner un temps précieux.

Architecture et assignation des variables

La K-Map à cinq variables étend le principe des versions à 4 variables. Imaginez une grille 4x4 (16 cellules) représentant les combinaisons de B,C,D,E. Les lignes utilisent B et C, les colonnes D et E. Ajoutez une cinquième variable A : on obtient deux grilles 4x4 côte à côte (32 cellules = 2⁵). La grille gauche correspond à A=0, la droite à A=1. Cette configuration préserve la logique familière tout en intégrant la variable supplémentaire.

Architecture de base d'une K-Map à 5 variables avec deux grilles 4x4

Différences avec les K-Map à 4 variables

Principales distinctions clés :

• Plus de cellules : 32 au lieu de 16 grâce à la 5ᵉ variable
• Double grille : Une pour A=0, l'autre pour A=1
• Adjacence trans-grilles : Les cellules homologues des deux grilles sont voisines
• Regroupements étendus : Jusqu'à 32 cellures regroupables

Pas de panique—l'idée de base du regroupement reste la même.

Étape 1 : Déterminer les variables

Identifiez vos cinq variables (A,B,C,D,E). Elles peuvent représenter des interrupteurs dans un circuit. Votre objectif : déterminer quand votre fonction booléenne est vraie (1) ou fausse (0) pour chaque combinaison.

Étape 2 : Étiqueter lignes et colonnes

Utilisez deux grilles 4x4. Étiquetez les lignes avec B et C en code Gray (00, 01, 11, 10). Les colonnes utilisent D et E avec le même code. Marquez la grille gauche comme A=0 et la droite comme A=1. Votre carte est prête !

Étape 3 : Remplir les cellules

Pour chaque combinaison A,B,C,D,E, insérez 1 ou 0 dans la grille correspondante (A=0 à gauche, A=1 à droite). Si vous disposez de minterms (combinaisons où la fonction vaut 1), placez simplement les 1 aux positions appropriées.

Règles de regroupement

La simplification passe par le regroupement des 1 selon ces règles :

• Taille des groupes : puissance de deux (1, 2, 4, 8, 16, 32)
• Formes : carrés ou rectangles (ex: 2x2, 1x4)
• Adjacence stricte entre cellules
• Privilégier les plus grands groupes possibles
• Chaque 1 doit appartenir à au moins un groupe

Exemple de regroupements valides dans une K-Map à 5 variables

Identifier les cellules adjacentes

Deux cellules sont adjacentes si elles diffèrent par une seule variable. À l'intérieur d'une grille : voisinage horizontal/vertical. Entre grilles : cellules homologues (même position mais A différent). Exemple : la cellule (00,00) de A=0 est adjacente à (00,00) de A=1.

Gestion des bordures connectées

Les bords des grilles sont connectés : première ligne reliée à la dernière, première colonne à la dernière. Ce principe s'applique aussi entre les deux grilles via la variable A. Cela permet des regroupements circulaires et trans-grilles pour maximiser les simplifications.

Exemple de cellules adjacentes (bordures colorées) dans une K-Map à 5 variables

Trouver les impliquants premiers

Un impliquant premier est un groupe maximal de 1s. Identifiez tous les groupes possibles puis éliminez ceux qui peuvent être fusionnés. Les groupes restants sont vos impliquants premiers - pièces maîtresses de la simplification.

Sélection des impliquants essentiels

Un impliquant est essentiel s'il contient un 1 non couvert ailleurs. Intégrez-les d'abord. Pour les 1s résiduels, choisissez des groupes complémentaires couvrant le maximum de 1s avec le moins de termes.

Écriture de l'expression minimale

Chaque groupe génère un terme :

• Variables constantes dans le groupe
• Variable = 1 ? Inclure tel quel (ex: B)
• Variable = 0 ? Inclure son complément (ex: B')
• Ignorer les variables variables

Combineze les termes avec des ET, puis les groupes avec des OU. Voilà votre expression simplifiée !

Exemple d'expression simplifiée depuis une K-Map à 5 variables

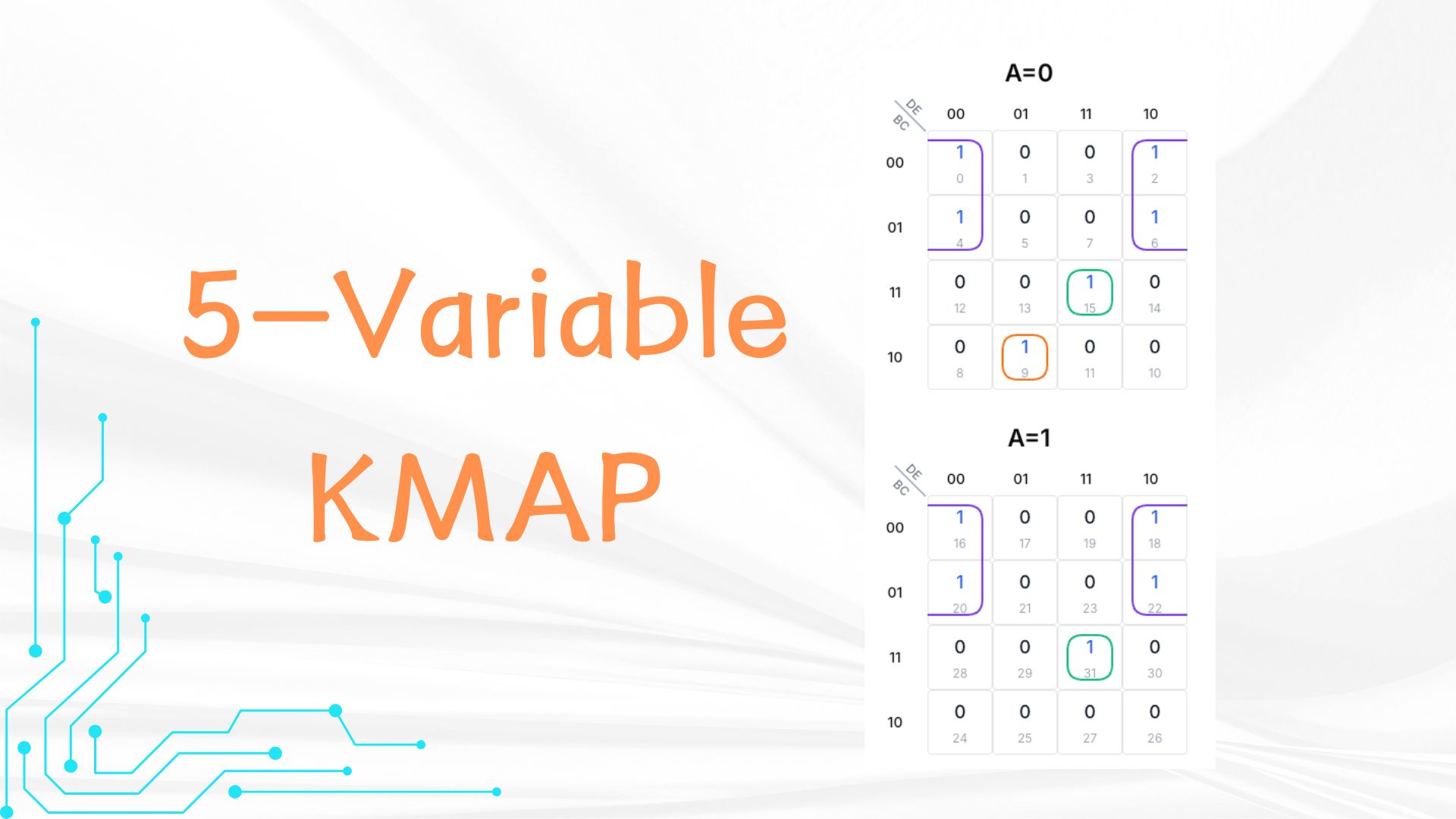
Prenons l'expression : A'B'C'D'E' + A'B'C'DE' + A'B'CD'E' + A'B'CDE' + A'BC'D'E + A'BCDE + AB'C'D'E' + AB'C'DE' + AB'CD'E' + AB'CDE' + ABCDE. En binaire : cellules 0,2,4,6,9,15,16,18,20,22,31.

Étape 1 : Remplissage

Grille A=0 :

• Ligne 00, colonne 00 : 1
• Ligne 00, colonne 01 : 1
• Ligne 01, colonne 11 : 1
• Ligne 01, colonne 10 : 1
• Ligne 11, colonne 11 : 1
• Ligne 10, colonne 01 : 1

In the A=1 grid, rows are also B and C (00, 01, 11, 10), columns are also D and E (00, 01, 11, 10). Put 1s:

• Ligne 00, colonne 00 : 1
• Ligne 00, colonne 01 : 1
• Ligne 01, colonne 11 : 1
• Ligne 01, colonne 10 : 1
• Ligne 11, colonne 11 : 1

K-Map à 5 variables remplie

Étape 2 : Regroupement

11 cellules à 1 : 6 dans A=0, 5 dans A=1.

• Groupe 1 : Terme unique A'BC'D'E
• Groupe 2 : 8 termes avec B' et E' constants
• Groupe 3 : 2 termes avec A variable

Exemple de regroupements dans une K-Map à 5 variables

Étape 3 : Simplification

• Groupe 1 : Conserver A'BC'D'E
• Groupe 2 : B'E' (variables constantes)
• Groupe 3 : BCDE (A indifférent)

Expression simplifiée : A'BC'D'E + B'E' + BCDE

Solution finale de l'exemple

Erreurs fréquentes à éviter

• Mauvais code Gray pour l'étiquetage
• Oublier les adjacences trans-grilles
• Regroupements non adjacents
• Groupes sous-optimaux
• Mauvaise identification des variables constantes

Bonnes pratiques

• Toujours utiliser le code Gray
• Prioriser les grands regroupements
• Vérifier les paires inter-grilles
• Couvrir tous les 1s
• Valider les termes avec la grille

Pour mettre en pratique, essayez notre Outil interactif de résolution de K-Map supportant jusqu'à 5 variables. Un excellent moyen de vérifier vos solutions et de gagner en confiance. Avec de la pratique, les K-Map à 5 variables deviendront aussi intuitives que celles à 4 variables !