Guide pratique et clair : Comment résoudre un K-Map à 4 variables

Qu'est-ce qu'un K-Map et son rôle en logique numérique

Le K-Map, abréviation de Karnaugh Map, permet de simplifier les expressions booléennes en logique numérique. Ces expressions agissent comme des instructions pour les circuits numériques, utilisant des valeurs vraies et fausses pour transformer les entrées en sorties. Leur simplification rend les circuits plus petits, rapides et économiques à fabriquer.

Le K-Map utilise une grille de carrés pour y parvenir. Dans une carte à 4 variables, elle contient 16 carrés. Chaque carré représente une combinaison unique de quatre entrées. Les carrés adjacents ne diffèrent que par une seule entrée. Cette configuration permet de repérer des motifs et de regrouper les sorties similaires pour simplifier l'expression.

La force des K-Maps réside dans leur aspect visuel et intuitif. Ils surpassent les méthodes mathématiques pures en réduisant les erreurs. Ils fonctionnent mieux avec 4 ou 5 variables, correspondant à la plupart des conceptions de circuits réels.

Comprendre la grille et l'affectation des variables

Un K-Map à 4 variables commence par une grille 4×4. Cette grille contient 16 carrés, un pour chaque combinaison possible de quatre entrées : A, B, C et D. Les lignes sont étiquetées avec des paires de A et B sur le côté. Les colonnes reçoivent des paires de C et D en haut. Nous remplissons ensuite chaque carré avec 1 ou 0 selon le problème logique, transformant ainsi le problème en image simplifiable.

Grille de K-Map 4 variables avec numéros de cellules (Minterms)

Importance du code Gray dans les K-Maps

Observez un K-Map à 4 variables. Les étiquettes des lignes et colonnes ne suivent pas l'ordre 00, 01, 10, 11 comme un comptage normal. Elles utilisent le code Gray : 00, 01, 11, 10. Ce n'est pas aléatoire. Le code Gray ne change qu'un seul bit à la fois. Par exemple, de 01 à 11, seul le premier bit change.

Ce détail est crucial. Chaque carré du K-Map représente une combinaison de variables. Les carrés voisins ne diffèrent que par une seule variable grâce au code Gray. Cela facilite le regroupement lors de la simplification. Sans code Gray, l'alignement serait incorrect et le regroupement difficile.

Convertir la fonction booléenne en minterms

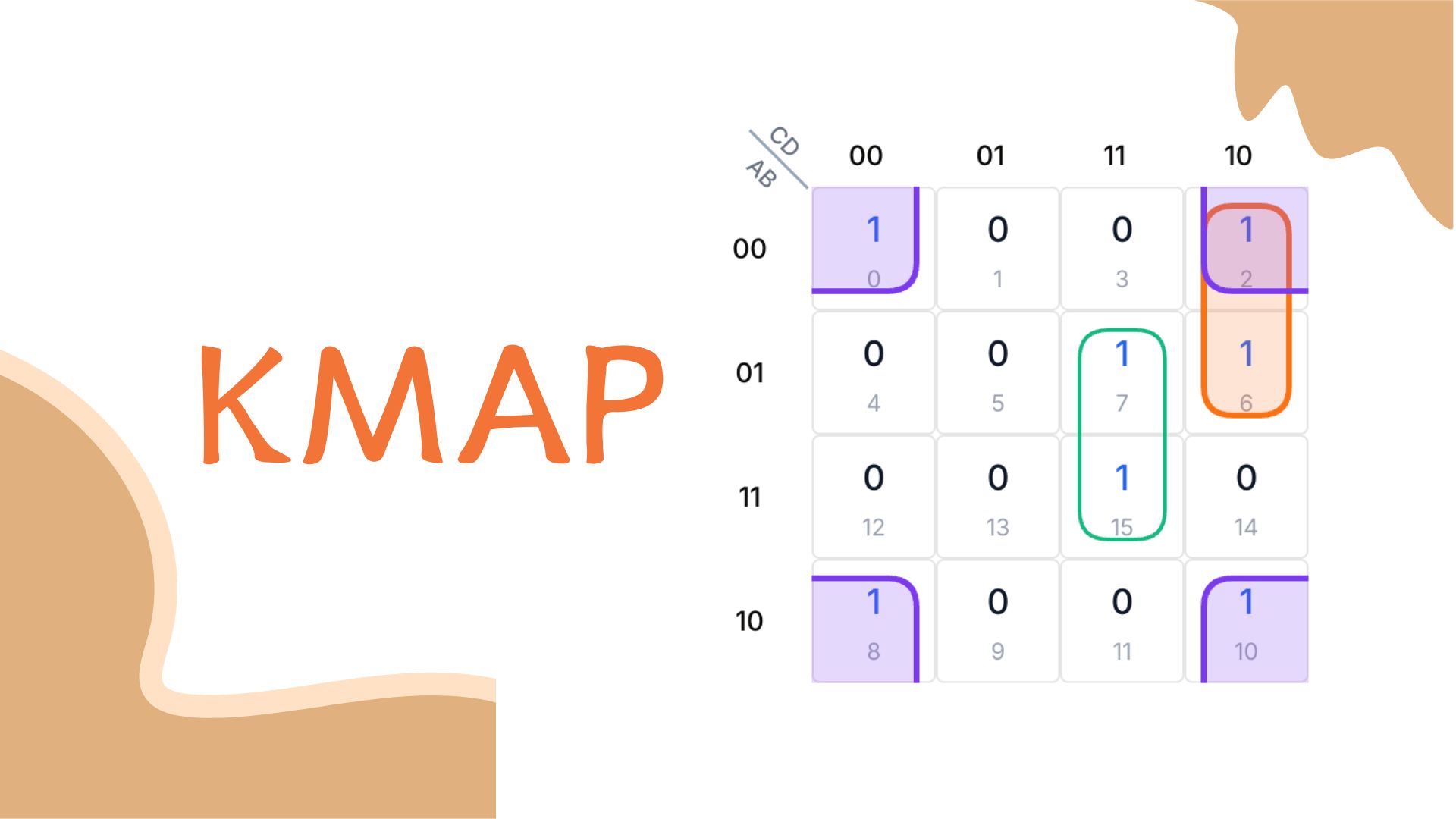
Pour utiliser un K-Map à 4 variables, nous identifions d'abord les combinaisons d'entrées qui rendent la fonction booléenne vraie. Ces combinaisons sont appelées minterms. Prenons cette fonction : F = A'B'C'D' + A'B'CD' + A'BC'D + A'BCD + AB'C'D' + AB'CD'. Chaque terme représente une combinaison de A, B, C et D donnant 1. Ces termes correspondent aux minterms 0, 2, 5, 7, 8 et 10.

Placer les minterms sur le K-Map

Ensuite, nous positionnons ces minterms sur la grille du K-Map. Chaque carré correspond à un numéro de minterm. Nous marquons un 1 dans les carrés des minterms 0, 2, 5, 7, 8 et 10. Tous les autres carrés restent à 0.

Placer les minterms sur le K-Map

Techniques de regroupement : taille, forme et position

Après avoir placé les minterms, nous regroupons les 1 sur le K-Map. Ce regroupement simplifie l'expression logique. Nous nous concentrons sur trois aspects : taille, forme et position. Examinons chacun.

Taille : privilégier les grands groupes

Nous formons des groupes aussi grands que possible. Un groupe peut contenir 1, 2, 4 ou 8 carrés. Les grands groupes simplifient davantage. Par exemple, un groupe de 4 est mieux qu'un groupe de 2. Nous visons à couvrir tous les 1 avec le moins de groupes possible.

Forme : respecter les rectangles

Les groupes doivent former des rectangles : ligne, colonne ou bloc 2x2. Les formes en L ou zigzag ne fonctionnent pas. Les rectangles maintiennent la logique simple et suivent les règles du K-Map.

Position : optimiser la grille

Nous positionnons les groupes pour couvrir efficacement le plus de 1. Les groupes peuvent s'étendre sur les bords, s'enrouler ou se chevaucher si utile. Cela clarifie la simplification.

Groupe de 2

Groupe de 4

Gérer les cas particuliers et les groupes enroulés

Certains 1 semblent éloignés sur le K-Map. Mais la grille s'enroule, connectant les bords opposés. Cela permet de regrouper des 1 apparemment distants. Voici comment cela fonctionne avec des exemples.

Bords qui se connectent

Imaginez des 1 sur les lignes supérieure et inférieure. Ils semblent séparés, mais le K-Map s'enroule verticalement. Cela relie le haut et le bas en un seul groupe. Idem pour les bords gauche et droit qui se connectent horizontalement.

Coins reliés

Visualisez des 1 dans les quatre coins : haut-gauche, haut-droit, bas-gauche, bas-droit. Ils semblent dispersés. Mais le K-Map s'enroule dans les deux sens, les unissant en un groupe de quatre.

Groupe horizontal

Groupe de bord

Interpréter les groupes pour former des termes produits

Après regroupement des 1, nous transformons chaque groupe en terme produit utilisant A, B, C et D. Nous identifions les variables constantes dans le groupe. Si une variable change, nous l'éliminons. Cela simplifie le terme. Voyons des exemples pour des groupes de 2, 4 et 8.

Groupe de 2 carrés

Prenons un groupe de deux carrés côte à côte. Exemple : AB'C'D + AB'CD. A reste 1, B reste 0, D reste 1, mais C passe de 0 à 1. Nous éliminons C. Le terme simplifié est AB'D.

Groupe de 2 carrés

Groupe de 2 simplifié

Groupe de 4 carrés

Prenons un bloc 2x2 de quatre carrés. Exemple : A'BC'D + A'BCD + ABC'D + ABCD. B reste 1, D reste 1, mais A et C changent. Nous éliminons A et C. Le terme simplifié est BD.

Groupe de 4 carrés

Groupe de 4 simplifié

Groupe de 8 carrés

Pour huit carrés (moitié de la carte). Exemple : A'B'C'D' + ... + A'BCD. A=0 reste constant, tandis que B, C et D varient. Seul A compte. Le terme est A'. Les grands groupes donnent des termes courts.

Groupe de 8 carrés

Groupe de 8 simplifié

Pourquoi la simplification fonctionne

Le regroupement simplifie en liant des combinaisons d'entrées. Si une variable change dans un groupe, cela n'affecte pas le motif. Nous l'éliminons et conservons les constantes. Chaque terme comme AB'D ou A' devient une partie simple de la solution.

Construire l'expression SOP finale

Nous combinons tous les termes produits avec des signes + pour former une expression SOP. Exemple : si nos groupes donnent AB'D, AD' et A', nous écrivons A' + AB'D + AD'. Voilà le résultat simplifié.

Quand considérer les groupes chevauchants

Parfois, un 1 peut appartenir à plusieurs groupes. C'est le chevauchement. Cela simplifie davantage. Utilisez-le quand un 1 ne s'intègre pas parfaitement à un groupe ou quand le partager réduit le nombre de termes.

Imaginez un 1 à la ligne 2, colonne 3. Il joint un groupe de quatre en ligne et un groupe de deux en colonne. Ce chevauchement peut simplifier l'expression finale.

Groupe chevauchant

Résumé du processus de simplification par K-Map

Simplifier avec un K-Map à 4 variables ressemble à résoudre un puzzle. Nous configurons une grille et plaçons les 1 de notre expression booléenne. Ensuite, nous regroupons ces 1 en rectangles de 1, 2, 4 ou 8 carrés. Visons les plus grands groupes possibles, pouvant s'enrouler sur les bords ou coins grâce au code Gray. Chaque groupe devient un terme simple. Moins de termes simplifient le résultat. Nous couvrons tous les 1 avec le moins de groupes et écrivons l'expression finale. C'est une méthode visuelle claire pour aborder la logique numérique.

Ressources pour s'entraîner davantage

Entraînez-vous avec des solveurs de table de Karnaugh interactifs qui visualisent le processus de simplification. Essayez notre Solveur de Table de Karnaugh pour expérimenter avec vos propres expressions booléennes.