Introducción
¿Qué es un mapa de Karnaugh?
¿Alguna vez te has preguntado cómo toman decisiones las computadoras? Utilizan algo llamado lógica booleana, que maneja valores verdaderos y falsos. Estas declaraciones pueden volverse complejas al combinarlas. Ahí es donde el mapa de Karnaugh, o K-Map, viene al rescate. Un K-Map es una herramienta visual que organiza estas expresiones lógicas en una cuadrícula ordenada. Esta disposición muestra todas las combinaciones posibles de variables, permitiéndonos identificar patrones rápidamente. Reconocer estos patrones nos ayuda a simplificar la lógica.
Si quieres profundizar en qué es un K-Map o cómo resolver un K-Map de 4 variables, consulta el artículo de referencia para más detalles: Cómo resolver un K-Map de 4 variables
¿Por qué usar un K-Map de cinco variables?
La mayoría de los K-Maps manejan dos, tres o cuatro variables. Pero a veces enfrentamos desafíos mayores con cinco variables. Imagina diseñar un circuito con cinco interruptores, cada uno puede estar activado o desactivado. ¡Son muchas combinaciones! Un K-Map de cinco variables nos ayuda a gestionar esta complejidad. Permite simplificar expresiones que serían difíciles de manejar de otra forma. Ya sea que estés construyendo un dispositivo o programando, este K-Map puede ahorrarte tiempo y esfuerzo.
Entendiendo la estructura del K-Map de cinco variables
Diseño y asignación de variables
Un K-Map de cinco variables puede sonar complejo, pero es una extensión de lo que ya conoces. Imagina un K-Map de cuatro variables: una cuadrícula 4x4 con 16 celdas. Cada celda representa combinaciones de cuatro variables como B,C,D,E. Las filas usan B y C, las columnas D y E. Al añadir una quinta variable A, necesitamos dos cuadrículas 4x4 (32 combinaciones, ya que 2⁵=32). Una cuadrícula representa A=0 y la otra A=1. En ambas, las filas siguen siendo B y C, y las columnas D y E. Esta estructura mantiene la familiaridad mientras maneja la variable adicional.

Diferencias con los K-Maps de cuatro variables
¿En qué se diferencia un K-Map de cinco variables? Analicemos las diferencias clave:
- Más celdas: 32 en lugar de 16 debido a la quinta variable
- Estructura dual: Dos cuadrículas para A=0 y A=1
- Adyacencia entre cuadrículas: Las celdas pueden ser vecinas entre ambas cuadrículas
- Grupos más grandes: Se pueden formar grupos hasta de 32 celdas
No te preocupes: la idea básica de agrupamiento sigue siendo la misma.
Cómo construir un K-Map de cinco variables
Paso 1: Determinar las variables
Comienza con tus cinco variables (A,B,C,D,E). Estas podrían representar interruptores en un circuito. Tu objetivo es determinar cuándo tu función booleana es verdadera (1) o falsa (0) para todas sus combinaciones.
Paso 2: Etiquetar filas y columnas
Configura dos cuadrículas 4x4. Etiqueta las filas en ambas con B y C usando código Gray (00,01,11,10). Las columnas usan D y E con el mismo código. Marca la cuadrícula izquierda como A=0 y la derecha como A=1. ¡Tu mapa está listo!
Paso 3: Llenar las celdas con valores
Asigna valores 1/0 según tu función. Para A=0 usa la cuadrícula izquierda, para A=1 la derecha. Si tienes minterms (combinaciones donde la función es 1), coloca 1s en esas celdas.
Cómo agrupar celdas en un K-Map de cinco variables
Reglas de agrupamiento
La simplificación ocurre agrupando 1s. Reglas clave:
- Grupos de tamaño potencia de dos: 1,2,4,8,16 o 32
- Formas cuadradas o rectangulares (ej. 2x2 o 1x4)
- Todas las celdas deben ser adyacentes
- Crea los grupos más grandes posibles
- Cada 1 debe estar en al menos un grupo

Identificando celdas adyacentes
Celdas son adyacentes si difieren en una variable. En cada cuadrícula, las celdas vecinas horizontal/vertical son adyacentes. Además, una celda en A=0 es adyacente a su equivalente en A=1. Esto permite grupos que cruzan ambas cuadrículas.
Manejo de continuidad en bordes
Los bordes del K-Map se conectan: la fila superior con la inferior, y columnas laterales. Además, las celdas pueden conectarse entre A=0 y A=1. Es como si el mapa se doblara para revelar más vecindades.

Simplificación de expresiones booleanas con K-Maps de 5 variables
Encontrando implicantes primos
Un implicante primo es un grupo máximo de 1s. Identifica todos los grupos posibles siguiendo las reglas, luego verifica que no puedan unirse con otros. Estos grupos maximales son tus implicantes primos.
Seleccionando implicantes primos esenciales
Algunos implicantes primos son obligatorios. Busca 1s que solo pertenezcan a un grupo. Incluye primero estos grupos esenciales. Para 1s restantes, selecciona grupos adicionales que cubran la mayoría con los menos grupos posibles.
Escribiendo la expresión mínima
Cada grupo genera un término:
- Identifica variables constantes en el grupo
- Incluye variables siempre en 1 (ej. B)
- Incluye negaciones para variables en 0 (ej. B')
- Omite variables que varían
Combina los términos con AND, luego une todos con OR. ¡Esa es tu expresión simplificada!

Ejemplos de simplificación con K-Map de 5 variables
Ejemplo: Expresión booleana A'B'C'D'E' + ... + ABCDE. En binario: celdas 00000(0), 00010(2), ..., 11111(31).
Paso 1: Llenar el K-Map
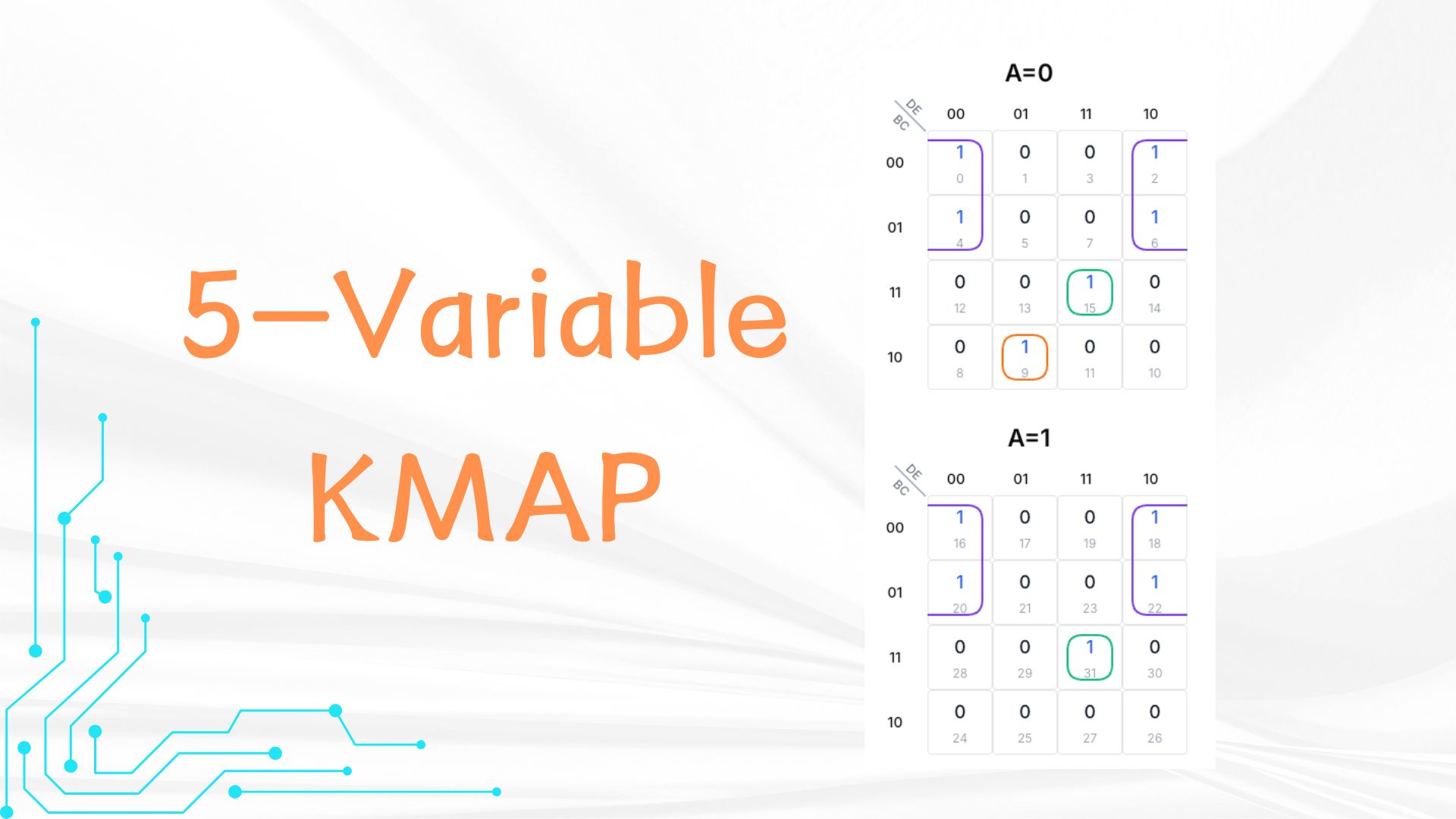
En cuadrícula A=0 (filas B,C y columnas D,E):
- Fila 00 (B=0,C=0), columna 00 (D=0,E=0): 1
- Fila 00 (B=0,C=0), columna 01 (D=1,E=0): 1
- Fila 01 (B=0,C=1), columna 11 (D=0,E=0): 1
- Fila 01 (B=0,C=1), columna 10 (D=1,E=0): 1
- Fila 11 (B=1,C=1), columna 11 (D=1,E=1): 1
- Fila 10 (B=1,C=0), columna 01 (D=0,E=1): 1
In the A=1 grid, rows are also B and C (00, 01, 11, 10), columns are also D and E (00, 01, 11, 10). Put 1s:
- Fila 00 (B=0,C=0), columna 00 (D=0,E=0): 1
- Fila 00 (B=0,C=0), columna 01 (D=1,E=0): 1
- Fila 01 (B=0,C=1), columna 11 (D=0,E=0): 1
- Fila 01 (B=0,C=1), columna 10 (D=1,E=0): 1
- Fila 11 (B=1,C=1), columna 11 (D=1,E=1): 1

Paso 2: Agrupar los 1s
Once 1s: seis en A=0 y cinco en A=1.
- Grupo 1: Término único: A'BC'D'E
- Grupo 2: A'B'C'D'E' + ... + AB'CDE'
- Grupo 3: A'BCDE + ABCDE

Paso 3: Simplificar
- Grupo 1: Mantener término único A'BC'D'E
- Grupo 2: B' y E' constantes → B'E'
- Grupo 3: A varía → BCDE
Expresión simplificada: A'BC'D'E + B'E' + BCDE

Consejos para dominar K-Maps de 5 variables
Errores comunes a evitar
- Etiquetas incorrectas: No usar código Gray
- Conexiones olvidadas: Ignorar adyacencias entre cuadrículas
- Agrupamientos erróneos: Celdas no adyacentes
- Grupos pequeños: No maximizar tamaños
- Términos incorrectos: Confundir variables constantes
Mejores prácticas para eficiencia
- Usa siempre código Gray
- Busca grupos grandes primero
- Revisa ambas cuadrículas para pares
- Asegura cobertura total de 1s
- Verifica términos contra la cuadrícula
¡Con estos pasos y consejos, estás listo para dominar K-Maps de 5 variables! Practica con nuestro solucionador interactivo de K-Maps que soporta hasta 5 variables. Es ideal para verificar tu trabajo y ganar confianza. ¡Sigue practicando!