Cómo resolver un K-Map de 4 variables: Una guía clara y práctica

Qué es un K-Map y su rol en lógica digital

El K-Map, abreviatura de Mapa de Karnaugh, ayuda a simplificar expresiones booleanas en lógica digital. Estas expresiones actúan como instrucciones para circuitos digitales, usando valores verdaderos y falsos para convertir entradas en salidas. Simplificarlas hace los circuitos más pequeños, rápidos y económicos de construir.

El K-Map utiliza una cuadrícula de celdas para lograrlo. En un mapa de 4 variables, tiene 16 celdas. Cada celda muestra una combinación única de cuatro entradas. Las celdas adyacentes difieren en solo una variable. Esta disposición permite identificar patrones y agrupar salidas similares para simplificar la expresión.

Los K-Maps destacan por ser visuales y fáciles de usar. Superan métodos matemáticos puros al reducir errores. Son más efectivos con 4 o 5 variables, adaptándose a la mayoría de diseños de circuitos reales.

Entendiendo la cuadrícula y asignación de variables

Un K-Map de 4 variables comienza con una cuadrícula 4×4. Tiene 16 celdas, una para cada combinación posible de cuatro entradas: A, B, C y D. Las filas se etiquetan con pares de A y B. Las columnas con pares de C y D. Llenamos cada celda con 1 o 0 según el problema lógico, transformándolo en una imagen simplificable.

Cuadrícula de K-Map de 4 variables con números de celda (Minterms)

Importancia del código Gray en K-Maps

Observa un K-Map de 4 variables. Las etiquetas no siguen 00, 01, 10, 11. Usan código Gray: 00, 01, 11, 10. Esto no es aleatorio. El código Gray cambia solo un bit por vez. Ejemplo: de 01 a 11, solo el primer bit cambia.

Esto es crucial. Cada celda muestra combinaciones donde celdas vecinas difieren en una variable, gracias al código Gray. Facilita agrupamientos al simplificar. Sin código Gray, los agrupamientos serían complicados.

Convirtiendo la función booleana a minterms

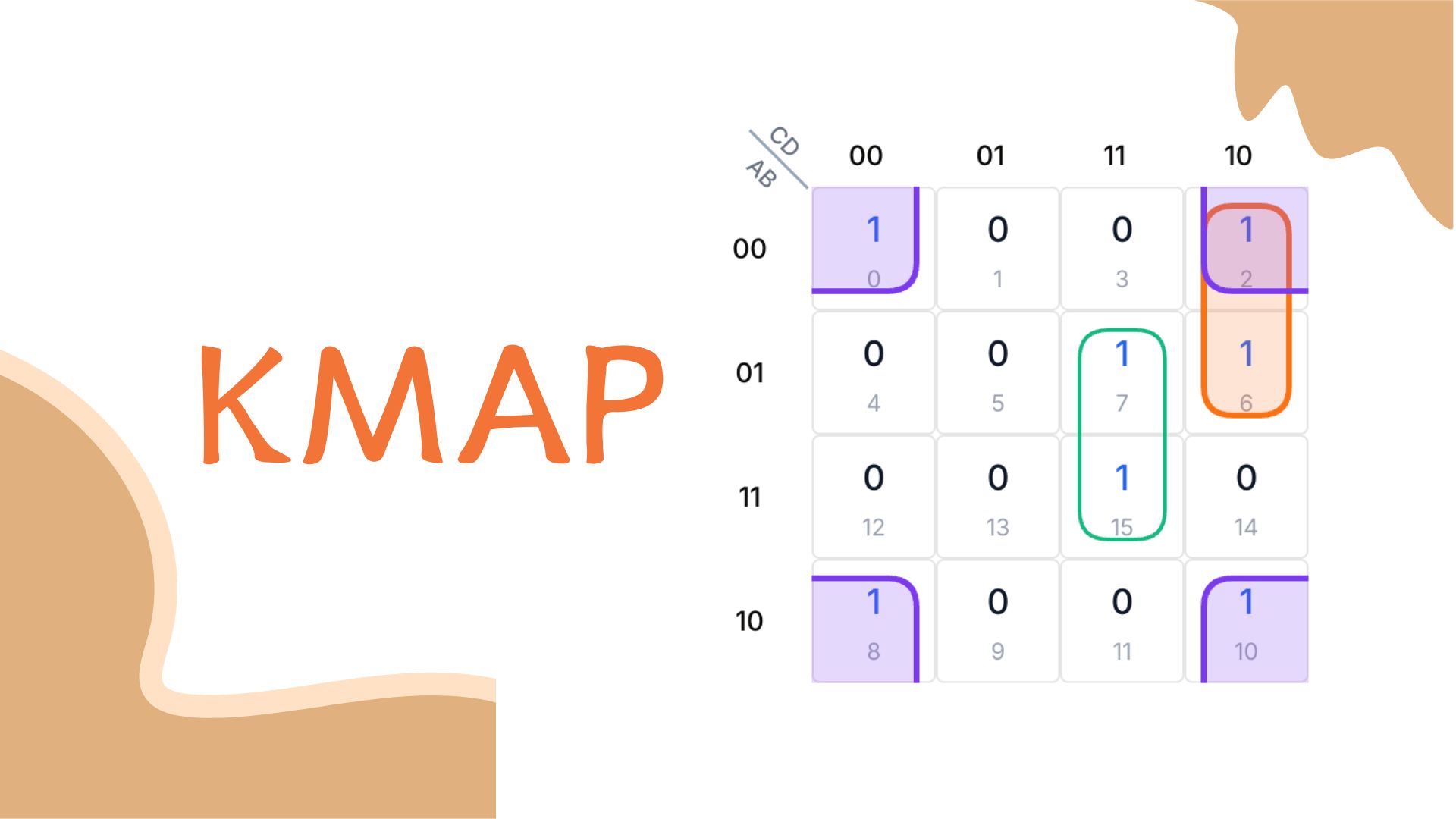
Para usar un K-Map de 4 variables, primero identificamos combinaciones que hacen verdadera la función booleana (minterms). Ejemplo: F = A'B'C'D' + A'B'CD' + A'BC'D + A'BCD + AB'C'D' + AB'CD'. Cada término corresponde a minterms 0, 2, 5, 7, 8 y 10.

Ubicando minterms en el K-Map

Luego, ubicamos estos minterms en la cuadrícula. Marcamos 1 en celdas correspondientes a minterms 0, 2, 5, 7, 8 y 10. Las demás permanecen en 0.

Minterms ubicados en el K-Map

Técnicas de agrupamiento: tamaño, forma y posición

Tras ubicar minterms, agrupamos los 1s. El agrupamiento simplifica la expresión. Consideramos tres aspectos:

Tamaño: prioriza grupos grandes

Creamos grupos lo más grandes posible (1, 2, 4 u 8 celdas). Grupos mayores simplifican más. Cubrimos todos los 1s con la menor cantidad de grupos.

Forma: mantén rectángulos

Los grupos deben ser rectángulos (filas, columnas o bloques 2x2). Formas irregulares no son válidas. Los rectángulos mantienen reglas del K-Map.

Posición: aprovecha la cuadrícula

Posicionamos grupos para cubrir 1s eficientemente. Pueden envolver bordes o superponerse si ayuda.

Grupo de 2

Grupo de 4

Manejando casos especiales y grupos envolventes

Algunos 1s parecen distantes, pero la cuadrícula se conecta en bordes opuestos. Esto permite agrupar 1s no adyacentes.

Bordes conectados

1s en filas superior e inferior parecen separados, pero el K-Map conecta verticalmente. Lo mismo aplica para bordes laterales.

Esquinas conectadas

1s en cuatro esquinas pueden agruparse gracias a la conexión horizontal y vertical simultánea.

Grupo horizontal

Grupo de borde

Interpretando grupos para formar términos producto

Cada grupo se convierte en término producto. Variables constantes en el grupo se mantienen; variables cambiantes se eliminan.

Grupo de 2 celdas

Ejemplo: AB'C'D + AB'CD. A=1, B'=0, D=1 permanecen. C varía, se elimina. Término simplificado: AB'D.

Grupo de 2 celdas

Grupo de 2 simplificado

Grupo de 4 celdas

Ejemplo: bloque 2x2. B=1, D=1 permanecen. A y C varían, se eliminan. Término: BD.

Grupo de 4 celdas

Grupo de 4 simplificado

Grupo de 8 celdas

Ocho celdas (mitad del mapa). Ejemplo: A' permanece constante. B, C, D varían. Término: A'.

Grupo de 8 celdas

Grupo de 8 simplificado

Por qué funciona la simplificación

Agrupar combina entradas equivalentes. Variables cambiantes no afectan el resultado, permitiendo eliminarlas.

Construyendo la expresión SOP final

Combinamos términos producto con signos +. Ejemplo: A' + AB'D + AD'. Resultado simplificado en forma SOP.

Cuándo considerar grupos superpuestos

Un 1 puede pertenecer a múltiples grupos. Útil cuando mejora la simplificación. Ejemplo: celda en fila 2, columna 3 puede estar en grupo horizontal y vertical simultáneamente.

La superposición reduce términos finales manteniendo cobertura completa.

Grupo superpuesto

Resumen del proceso de simplificación con K-Map

Simplificar con K-Map de 4 variables es como resolver un rompecabezas. Configuramos la cuadrícula, ubicamos minterms, agrupamos 1s en rectángulos maximizando tamaño, y derivamos términos simplificados. La conexión de bordes y esquinas permite agrupamientos inteligentes.

Recursos para práctica adicional

Practica con simuladores interactivos de K-Map que visualicen el proceso de simplificación. Prueba nuestro Solucionador de K-Map para experimentar con tus propias expresiones booleanas.