Einführung
Was ist ein Karnaugh-Diagramm?
Hast du dich schon mal gefragt, wie Computer Entscheidungen treffen? Sie verwenden boolesche Logik, die mit wahr- und falsch-Werten arbeitet. Diese logischen Aussagen können richtig knifflig werden, wenn wir sie kombinieren. Hier kommt das Karnaugh-Diagramm (K-Map) ins Spiel. Ein K-Map ist ein praktisches Werkzeug, das diese logischen Aussagen in ein übersichtliches Raster bringt. Das Raster zeigt alle möglichen Kombinationen von Variablen, sodass wir Muster schnell erkennen können. Diese Muster helfen uns, die Logik zu vereinfachen.
Wenn du mehr über K-Maps oder das Lösen eines 4-Variablen-K-Maps erfahren möchtest, wirf einen Blick in den Referenzartikel: Anleitung zum Lösen eines 4-Variablen-K-Maps
Warum ein 5-Variablen-K-Map verwenden?
Die meisten K-Maps handhaben zwei, drei oder vier Variablen. Aber manchmal brauchen wir mehr – fünf Variablen. Stell dir vor, du entwirfst eine Schaltung mit fünf Schaltern – jeder kann ein- oder ausgeschaltet sein. Das sind jede Menge Kombinationen! Ein 5-Variablen-K-Map hilft, diese Komplexität zu meistern. Es vereinfacht Ausdrücke, die sonst schwer zu handhaben wären. Ob Schaltungsdesign oder Programmierung – ein 5-Variablen-K-Map spart Zeit und Nerven.
Aufbau eines 5-Variablen-K-Maps
Struktur und Variablenzuordnung
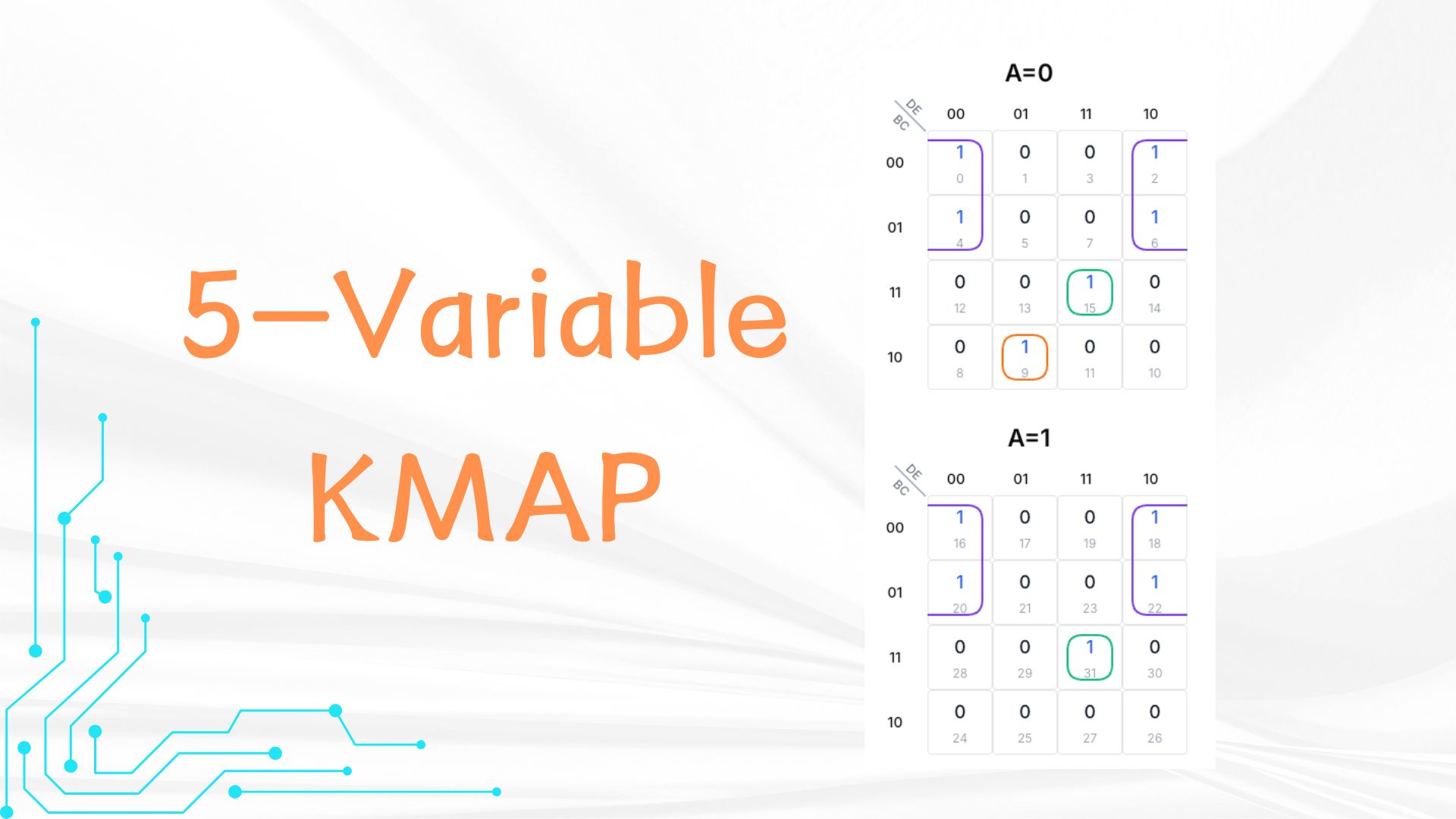
Ein 5-Variablen-K-Map klingt komplex, ist aber nur eine Erweiterung des Bekannten. Ein 4-Variablen-K-Map ist ein 4x4-Raster mit 16 Zellen. Jede Zelle repräsentiert eine Kombination von vier Variablen wie B,C,D,E. Die Zeilen verwenden B und C, die Spalten D und E. Füge nun eine fünfte Variable A hinzu. Für alle 32 Kombinationen (2⁵ = 32) brauchen wir zwei 4x4-Raster nebeneinander. Ein Raster für A=0, das andere für A=1. In jedem Raster bleiben Zeilen (B,C) und Spalten (D,E) gleich – so bleibt die Struktur vertraut.

Unterschiede zu 4-Variablen-K-Maps
Was unterscheidet ein 5-Variablen-K-Map? Hier die Hauptunterschiede:
- Mehr Zellen: 32 statt 16 durch die fünfte Variable
- Doppeltes Raster: Zwei Raster für A=0 und A=1
- Übergreifende Nachbarschaft: Zellen können zwischen den Rastern benachbart sein
- Größere Gruppen: Bis zu 32 Zellen gruppierbar
Keine Sorge – das Grundprinzip des Gruppierens bleibt gleich.
Aufbau eines 5-Variablen-K-Maps
Schritt 1: Variablen festlegen
Starte mit fünf Variablen (z.B. A,B,C,D,E). Diese könnten Schalter in einer Schaltung repräsentieren. Deine Aufgabe: Bestimme, wann die boolesche Funktion wahr (1) oder falsch (0) ist.
Schritt 2: Zeilen und Spalten beschriften
Richte zwei 4x4-Raster ein. Beschrifte die Zeilen beider Raster mit B und C im Gray-Code (00, 01, 11, 10). Spalten beschriftest du mit D und E ebenfalls im Gray-Code. Markiere das linke Raster als A=0, das rechte als A=1.
Schritt 3: Zellen mit Funktionswerten füllen
Trage für jede Variablenkombination 1 oder 0 ein. Bei A=0 im linken Raster, bei A=1 im rechten. Hast du Minterms (Kombinationen mit 1), trage diese ein.
Zellengruppierung im 5-Variablen-K-Map
Gruppierungsregeln
Vereinfachung durch Gruppieren von 1ern. Die Regeln:
- Gruppengröße muss Zweierpotenz sein: 1,2,4,8,16,32
- Gruppen müssen rechteckig oder quadratisch sein
- Alle Zellen müssen benachbart sein
- Größtmögliche Gruppen bilden
- Jede 1 muss in mindestens einer Gruppe sein

Benachbarte Zellen identifizieren
Zellen sind benachbart, wenn sie sich nur in einer Variable unterscheiden. Innerhalb der Raster gelten horizontale/vertikale Nachbarn. Zusätzlich sind gleiche Positionen in A=0 und A=1 Rastern benachbart – nur A ändert sich. So können Gruppen beide Raster umspannen.
Umschließende Kanten bei 5 Variablen
K-Maps haben einen cleveren Trick: Die Ränder sind verbunden. Oberste Zeile verbindet mit unterster, linke mit rechter Spalte. Zusätzlich verbinden sich gleiche Positionen zwischen A=0 und A=1. So entstehen kreuzübergreifende Gruppen.

Boolesche Ausdrücke mit 5-Variablen-K-Maps vereinfachen
Primimplikanten finden
Ein Primimplikant ist eine maximal große Gruppe von 1ern. Finde alle möglichen Gruppen und prüfe, ob sie nicht erweiterbar sind. Diese maximalen Gruppen sind deine Bausteine für die vereinfachte Formel.
Essenzielle Primimplikanten auswählen
Essenzielle Gruppen enthalten 1er, die nur in einer Gruppe vorkommen. Diese müssen zuerst ausgewählt werden. Für übrige 1er wähle Gruppen, die möglichst viele abdecken.
Minimalen Ausdruck formulieren
So leitest du Terme ab:
- Finde konstant bleibende Variablen in der Gruppe
- Immer 1? Variable hinzufügen (z.B. B)
- Immer 0? Negation hinzufügen (z.B. B')
- Variables Variablen überspringen
Verknüpfe alle Terme durch ODER-Operatoren – das ist dein vereinfachter Ausdruck!

Beispiele zur 5-Variablen-K-Map-Vereinfachung
Beispiel: Boolescher Ausdruck A'B'C'D'E' + ... + ABCDE. Binär entspricht das den Zellen 00000, 00010, ..., 11111.
Schritt 1: K-Map füllen
Im A=0-Raster: Zeilen B,C (Gray-Code), Spalten D,E. Setze 1er an:
- Zeile 00 (B=0,C=0), Spalte 00 (D=0,E=0): 1
- Zeile 00 (B=0,C=0), Spalte 01 (D=1,E=0): 1
- Zeile 01 (B=0,C=1), Spalte 11 (D=0,E=0): 1
- Zeile 01 (B=0,C=1), Spalte 10 (D=1,E=0): 1
- Zeile 11 (B=1,C=1), Spalte 11 (D=1,E=1): 1
- Zeile 10 (B=1,C=0), Spalte 01 (D=0,E=1): 1
In the A=1 grid, rows are also B and C (00, 01, 11, 10), columns are also D and E (00, 01, 11, 10). Put 1s:
- Zeile 00 (B=0,C=0), Spalte 00 (D=0,E=0): 1
- Zeile 00 (B=0,C=0), Spalte 01 (D=1,E=0): 1
- Zeile 01 (B=0,C=1), Spalte 11 (D=0,E=0): 1
- Zeile 01 (B=0,C=1), Spalte 10 (D=1,E=0): 1
- Zeile 11 (B=1,C=1), Spalte 11 (D=1,E=1): 1

Schritt 2: 1er gruppieren
Elf 1er: Sechs im A=0-Raster, fünf im A=1-Raster.
- Gruppe 1: Einzelterm A'BC'D'E
- Gruppe 2: A'B'C'D'E' + ... + AB'CDE'
- Gruppe 3: A'BCDE + ABCDE

Schritt 3: Vereinfachen
- Gruppe 1: Einzelterm A'BC'D'E
- Gruppe 2: Konstante B' und E' → B'E'
- Gruppe 3: A ändert sich → BCDE
Vereinfachter Ausdruck: A'BC'D'E + B'E' + BCDE

Tipps für 5-Variablen-K-Maps
Häufige Fehler
- Falsche Gray-Code-Beschriftung
- Übergreifende Nachbarschaft vergessen
- Nicht-benachbarte Zellen gruppieren
- Zu kleine Gruppen bilden
- Falsche Variablen in Termen
Beste Praktiken
- Immer Gray-Code verwenden
- Größte Gruppen zuerst suchen
- Beide Raster auf Paare prüfen
- Jede 1 muss gruppiert sein
- Terme anhand des Rasters prüfen
Probiere unser interaktives K-Map Solver Tool für bis zu 5 Variablen aus. Perfekt zum Üben und Ergebnisprüfen!