Wie man ein 4-Variablen-K-Map löst: Eine Schritt-für-Schritt-Anleitung
Was ist eine K-Map und ihre Rolle in der Digitaltechnik
K-Map, kurz für Karnaugh Map, hilft bei der Vereinfachung boolescher Ausdrücke in der Digitaltechnik. Diese Ausdrücke wirken wie Anweisungen für digitale Schaltkreise, verwenden Wahrheitswerte und wandeln Eingaben in Ausgaben um. Durch Vereinfachung werden Schaltkreise kleiner, schneller und kostengünstiger.
K-Map verwendet ein Raster aus Quadraten. Eine 4-Variable-Map hat 16 Quadrate. Jedes Quadrat zeigt eine einzigartige Kombination von vier Eingängen. Benachbarte Quadrate unterscheiden sich nur durch eine Variable. Dies ermöglicht das Erkennen von Mustern und das Gruppieren ähnlicher Ausgaben.
K-Maps glänzen durch ihre visuelle Darstellung und Benutzerfreundlichkeit. Sie reduzieren Fehler im Vergleich zu rein mathematischen Methoden und eignen sich optimal für 4-5 Variablen - perfekt für reale Schaltungsdesigns.
K-Maps wurden 1953 von Maurice Karnaugh auf Basis von Edward Veitchs Arbeit eingeführt und sind heute unverzichtbar im digitalen Schaltungsdesign.
Aufbau der 4-Variablen-K-Map
Rasterverständnis und Variablenzuordnung
Eine 4-Variablen-K-Map beginnt mit einem 4×4-Raster. Die Zeilen zeigen A/B-Kombinationen, Spalten C/D-Kombinationen. Jedes Quadrat wird mit 1 oder 0 befüllt - dies visualisiert das Logikproblem zur Vereinfachung.

Bedeutung des Gray-Codes in K-Maps
Die Zeilen- und Spaltenbeschriftungen folgen nicht der normalen Binärfolge, sondern dem Gray-Code (00, 01, 11, 10). Gray-Code ändert pro Schritt nur ein Bit - entscheidend für korrektes Gruppieren.
Dank Gray-Code unterscheiden sich benachbarte Quadrate nur durch eine Variable. Dies ermöglicht einfache Gruppierungen - ohne Gray-Code wäre die Vereinfachung fehleranfällig.
Binärcode
Gray-Code
Funktion eintragen
Umwandlung der Booleschen Funktion in Minterms
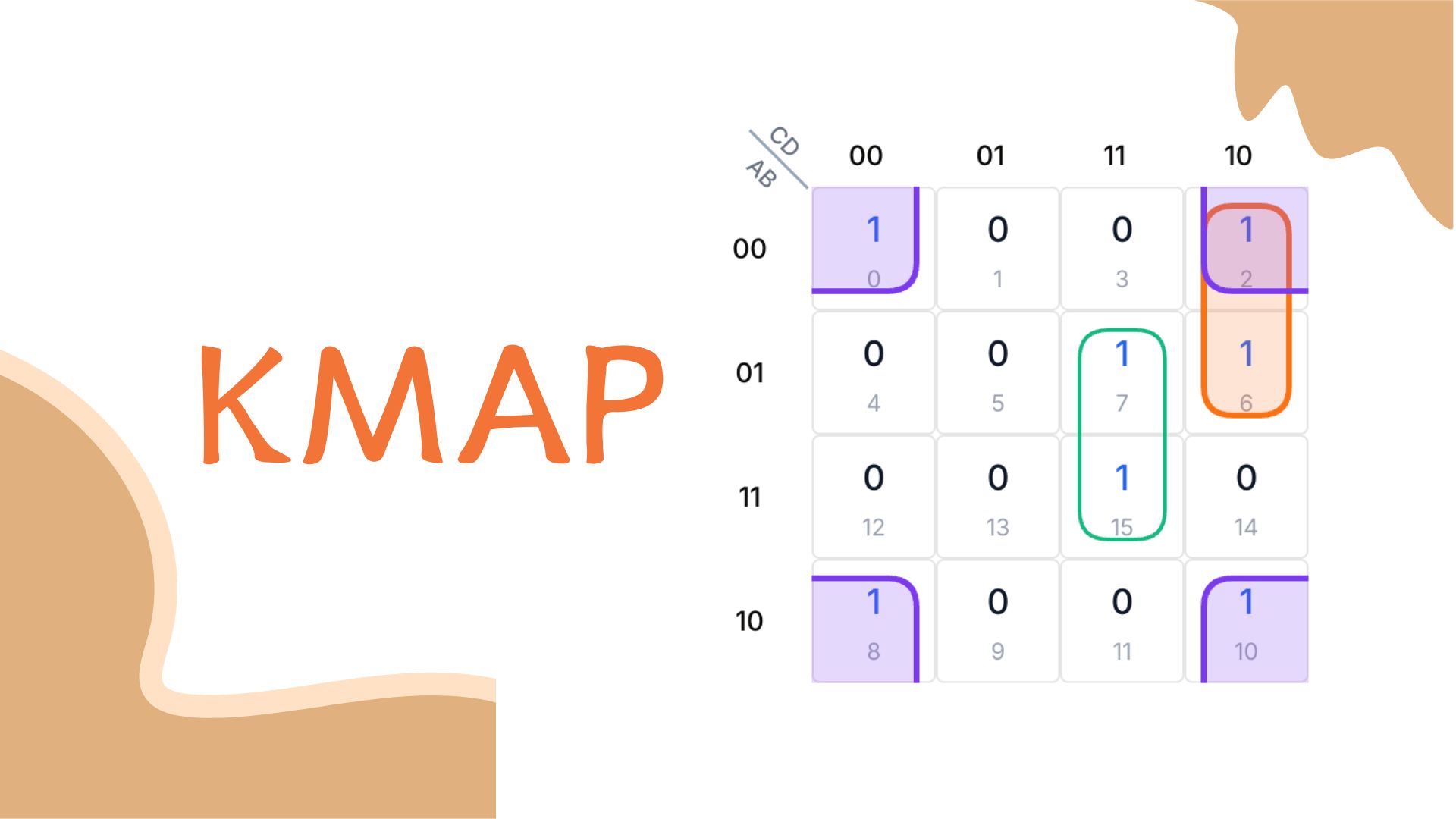
Wir identifizieren Eingabekombinationen, die die Boolesche Funktion wahr machen (Minterms). Beispiel: F = A'B'C'D' + ... entspricht Minterms 0, 2, 5, 7, 8, 10.
F(A,B,C,D) = A'B'C'D' + A'B'CD' + A'BC'D + A'BCD + AB'C'D' + AB'CD'
= Σm(0,2,5,7,8,10)
Minterms in der K-Map markieren
Minterm-Nummern werden im Raster durch 1en gekennzeichnet. Nicht genutzte Felder bleiben bei 0.

Funktionsvereinfachung
Gruppierungstechniken: Größe, Form, Position
Gruppieren der 1er-Felder folgt drei Prinzipien:
Größe: Maximale Gruppen bilden
Gruppengrößen von 1, 2, 4 oder 8 Quadraten anstreben. Größere Gruppen = einfachere Terme.
Form: Rechtecke bevorzugen
Nur rechteckige Blöcke (Zeilen, Spalten, 2x2-Blöcke) sind gültig - keine L-Formen oder Zickzacks.
Position: Intelligente Platzierung
Gruppen können über Kanten laufen oder sich überlappen, um maximale Abdeckung zu erreichen.

Gruppe von 2

Gruppe von 4
Sonderfälle und Wrap-Around-Gruppen
Das Raster ist zyklisch - gegenüberliegende Kanten verbinden sich:
Verbundene Kanten
1er an Ober- und Unterkante bilden eine durchgehende Gruppe.
Verknüpfte Ecken
Alle vier Eck-1er bilden eine 4er-Gruppe durch zyklische Verbindung.

Horizontale Gruppe

Kantengruppe
Ableitung des vereinfachten Ausdrucks
Gruppeninterpretation für Produktterme
Jede Gruppe wird zu einem Produktterm reduziert:
2er-Gruppe
Beispiel: AB'D entsteht durch Weglassen der variierenden Variable C.

2er-Gruppe

Vereinfachte 2er-Gruppe
4er-Gruppe
Beispiel: BD entsteht durch Eliminierung zweier variierender Variablen.

4er-Gruppe

Vereinfachte 4er-Gruppe
8er-Gruppe
Beispiel: A' entsteht, da nur diese Variable konstant bleibt.

8er-Gruppe

Vereinfachte 8er-Gruppe
Warum Vereinfachung funktioniert
Variablenänderungen innerhalb der Gruppe werden eliminiert - nur Konstanten bleiben erhalten.
Erstellung des finalen SOP-Ausdrucks
Alle Produktterme werden mit + zu einer Summe der Produkte (SOP) kombiniert, z.B. A' + AB'D + AD'.
Fortgeschrittene Gruppierungsstrategien
Überlappende Gruppen nutzen
Einzelne 1er können mehreren Gruppen angehören, um die Termanzahl zu minimieren.
Beispiel: Ein Quadrat in Zeile 2, Spalte 3 kann gleichzeitig zu horizontaler und vertikaler Gruppe gehören.

Überlappende Gruppe
Zusammenfassung
Zusammenfassung des K-Map-Vereinfachungsprozesses
K-Map-Vereinfachung ist ein visuelles Puzzle: Raster aufbauen, 1er eintragen, maximale Rechtecksgruppen bilden (ggf. über Kanten), Terme ableiten und kombinieren.
Kernpunkte
- 1Rasterstruktur und Variablenzuordnung verstehen
- 2Minterms korrekt eintragen
- 3Größtmögliche Gruppen bilden
- 4Vereinfachten Ausdruck aus Gruppen ableiten
Ressourcen für weitere Übungen
Üben Sie mit interaktiven K-Map-Lösern, die den Vereinfachungsprozess visualisieren. Probieren Sie unseren K-Map-Löser aus, um mit Ihren eigenen booleschen Ausdrücken zu experimentieren.