4변수 K-Map 풀이 방법: 명확하고 실용적인 가이드

4변수 K-Map 풀이 방법: 단계별 가이드

K-Map이란 무엇이며 디지털 논리에서의 역할

K-Map(카르노 맵)은 디지털 논리에서 부울 표현식을 단순화하는 데 도움을 줍니다. 이러한 표현식은 입력을 출력으로 변환하기 위해 참과 거짓 값을 사용하는 디지털 회로의 지침 역할을 합니다. 이를 단순화하면 회로를 더 작고 빠르며 제작 비용을 절감할 수 있습니다.

K-Map은 사각형 격자를 사용하여 이를 수행합니다. 4변수 맵은 16개의 사각형으로 구성되며, 각 사각형은 네 가지 입력의 고유한 조합을 나타냅니다. 인접한 사각형들은 단 하나의 입력만 다른 특성을 가지며, 이 구조 덕분에 패턴을 식별하고 유사한 출력을 그룹화하여 표현식을 단순화할 수 있습니다.

K-Map은 시각적이며 사용하기 쉬워 순수 수학적 방법보다 오류를 줄이는 데 효과적입니다. 대부분의 실제 회로 설계에 적합한 4~5변수에서 특히 빛을 발합니다.

K-Map은 1953년 Maurice Karnaugh가 Edward Veitch의 연구를 기반으로 도입했으며, 이후 디지털 회로 설계의 필수 도구로 자리매김했습니다.

4변수 K-Map 설정 방법

격자 구조와 변수 할당 이해

4변수 K-Map은 4×4 격자로 시작합니다. 이 격자는 A, B, C, D 네 가지 입력의 가능한 모든 조합에 해당하는 16개의 사각형을 포함합니다. 행에는 A와 B 조합을, 열에는 C와 D 조합을 배치합니다. 각 사각형에 논리 문제에 따라 1 또는 0을 채워 시각적 단순화를 수행합니다.

민텀 표시가 있는 4변수 K-Map 격자

K-Map에서 그레이 코드의 중요성

4변수 K-Map의 행과 열 레이블은 일반적인 00, 01, 10, 11 순서가 아닌 그레이 코드(00, 01, 11, 10)를 사용합니다. 이는 무작위가 아닌 한 번에 한 비트만 변경되는 특성으로, 예를 들어 01에서 11로 이동할 때 첫 번째 비트만 변경됩니다.

이 특성은 K-Map에서 인접 사각형들이 단 하나의 변수만 다르도록 배치되어 그룹화를 용이하게 합니다. 그레이 코드 없이는 사각형 정렬이 어려워 단순화 과정이 복잡해집니다.

이진 코드

00011011

이진 코드 순서

그레이 코드

00011110

그레이 코드 순서

함수 표시 방법

부울 함수를 민텀으로 변환

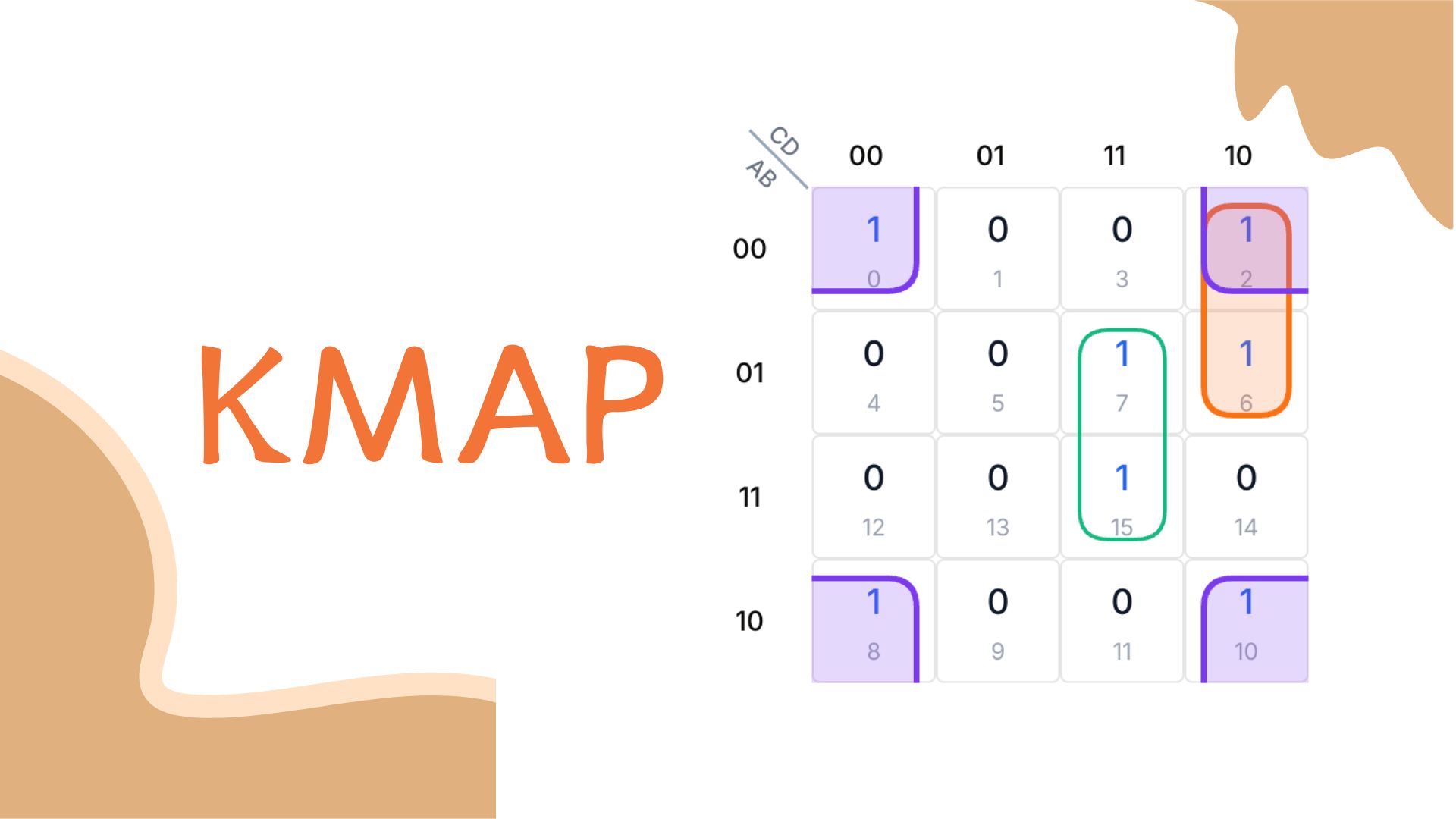
4변수 K-Map 사용 시 먼저 부울 함수가 참이 되는 입력 조합(민텀)을 찾습니다. 예시 함수 F = A'B'C'D' + A'B'CD' + A'BC'D + A'BCD + AB'C'D' + AB'CD'에서 각 항은 1을 출력하는 조합에 해당하며, 이는 민텀 0, 2, 5, 7, 8, 10과 일치합니다.

F(A,B,C,D) = A'B'C'D' + A'B'CD' + A'BC'D + A'BCD + AB'C'D' + AB'CD'

= Σm(0,2,5,7,8,10)

SOP 형식의 부울 함수 및 민텀 표기법