Introduzione
Cos'è una Mappa di Karnaugh?
Ti sei mai chiesto come i computer prendono decisioni? Utilizzano una logica booleana, che lavora con valori vero/falso. Queste condizioni possono diventare complesse quando combinate. Ecco che entra in gioco la mappa di Karnaugh, o K-Map, per semplificare il tutto. Si tratta di uno strumento visivo che organizza le espressioni logiche in una griglia ordinata. Questa disposizione mostra tutte le possibili combinazioni di variabili, permettendoci di identificare rapidamente schemi ricorrenti. Riconoscere questi pattern ci aiuta a semplificare la logica sottostante.
Per approfondire il funzionamento delle K-Map o imparare a risolvere una mappa a 4 variabili, consulta l'articolo di riferimento:: Come Risolvere una K-Map a 4 Variabili
Perché Usare una K-Map a 5 Variabili?
Le K-Map standard gestiscono 2-4 variabili, ma sfide più complesse richiedono 5 variabili. Immagina di progettare un circuito con 5 interruttori - ognuno può essere acceso o spento. Le combinazioni possibili diventano esponenziali! Una K-Map a 5 variabili aiuta a gestire questa complessità, semplificando espressioni altrimenti ingestibili. Che tu stia costruendo un dispositivo o scrivendo codice, questo strumento ti farà risparmiare tempo e fatica.
Struttura della K-Map a 5 Variabili
Layout e Assegnazione Variabili
Una K-Map a 5 variabili è un'estensione della versione a 4 variabili. Parti dalla griglia 4x4 classica (16 celle) per le variabili B,C,D,E. Aggiungi la quinta variabile A utilizzando due griglie affiancate: sinistra per A=0, destra per A=1. In ogni griglia, le righe rappresentano B e C in codice Gray (00,01,11,10), le colonne D ed E con lo stesso codice. Questa struttura mantiene la familiarità pur gestendo 32 combinazioni (2⁵).

Differenze dalle K-Map a 4 Variabili
Ecco le principali differenze:
- Più celle: 32 invece di 16 per la quinta variabile
- Doppia griglia: Separazione A=0 e A=1
- Adiacenza trasversale: Celle equivalenti nelle due griglie sono vicine
- Gruppi più ampi: Fino a 32 celle raggruppabili
Il principio di base del raggruppamento rimane invariato.
Costruire una K-Map a 5 Variabili
Step 1: Identificare le Variabili
Definisci le 5 variabili (A,B,C,D,E). Determina quando la tua funzione booleana è vera (1) o falsa (0) per ogni combinazione.
Step 2: Etichettatura Griglie
Prepara due griglie 4x4. Etichetta righe con B e C in codice Gray (00,01,11,10). Colonne con D ed E stesso codice. Marca la griglia sinistra come A=0 e destra come A=1.
Step 3: Compilazione Celle
Inserisci 1 o 0 in ogni cella in base alla funzione. Per A=0 usa la griglia sinistra, per A=1 quella destra. Se disponi di mintermini (combinazioni con output 1), posiziona gli 1 corrispondenti.
Raggruppamento Celle in K-Map 5V
Regole di Raggruppamento
Semplifica raggruppando gli 1 seguendo queste regole:
- Dimensioni gruppo: Potenze di due (1,2,4,8,16,32)
- Forma: Quadrati/rettangoli (es. 2x2, 1x4)
- Celle adiacenti (spiegato sotto)
- Massimizza le dimensioni dei gruppi
- Ogni 1 deve appartenere ad almeno un gruppo

Identificare Celle Adiacenti
Due celle sono adiacenti se differiscono per una sola variabile. Oltre all'adiacenza orizzontale/verticale dentro una griglia, le celle nella stessa posizione tra A=0 e A=1 sono vicine. Es: cella (00,00) in A=0 è adiacente a (00,00) in A=1.
Gestione dei Bordi
Le K-Map permettono avvolgimenti: il bordo superiore connette con l'inferiore, sinistro con destro. Inoltre, grazie alle due griglie, è possibile raggruppare celle equivalenti tra A=0 e A=1. Immagina una mappa che si ripiega su sé stessa per massimizzare le connessioni.

Semplificazione Espressioni con K-Map 5V
Trovare Implicanti Primi
Un implicante primo è un gruppo massimale di 1s. Identifica tutti i gruppi possibili rispettando le regole, assicurandoti che non possano essere uniti ad altri per formare gruppi più grandi. Questi saranno i mattoni della tua espressione semplificata.
Selezionare Implicanti Essenziali
Gli implicanti essenziali contengono almeno un 1 coperto solo dal loro gruppo. Includili per primi. Se rimangono 1 scoperti, aggiungi gruppi aggiuntivi che coprano il maggior numero residuo con il minor numero di termini.
Scrittura Espressione Minimale
Ogni gruppo genera un termine:
- Identifica variabili costanti nel gruppo
- Includi variabili sempre a 1 (es. B)
- Includi negazioni per variabili sempre a 0 (es. B')
- Ignora variabili che cambiano
Combina i termini con OR per ottenere l'espressione finale semplificata.

Esempi di Semplificazione
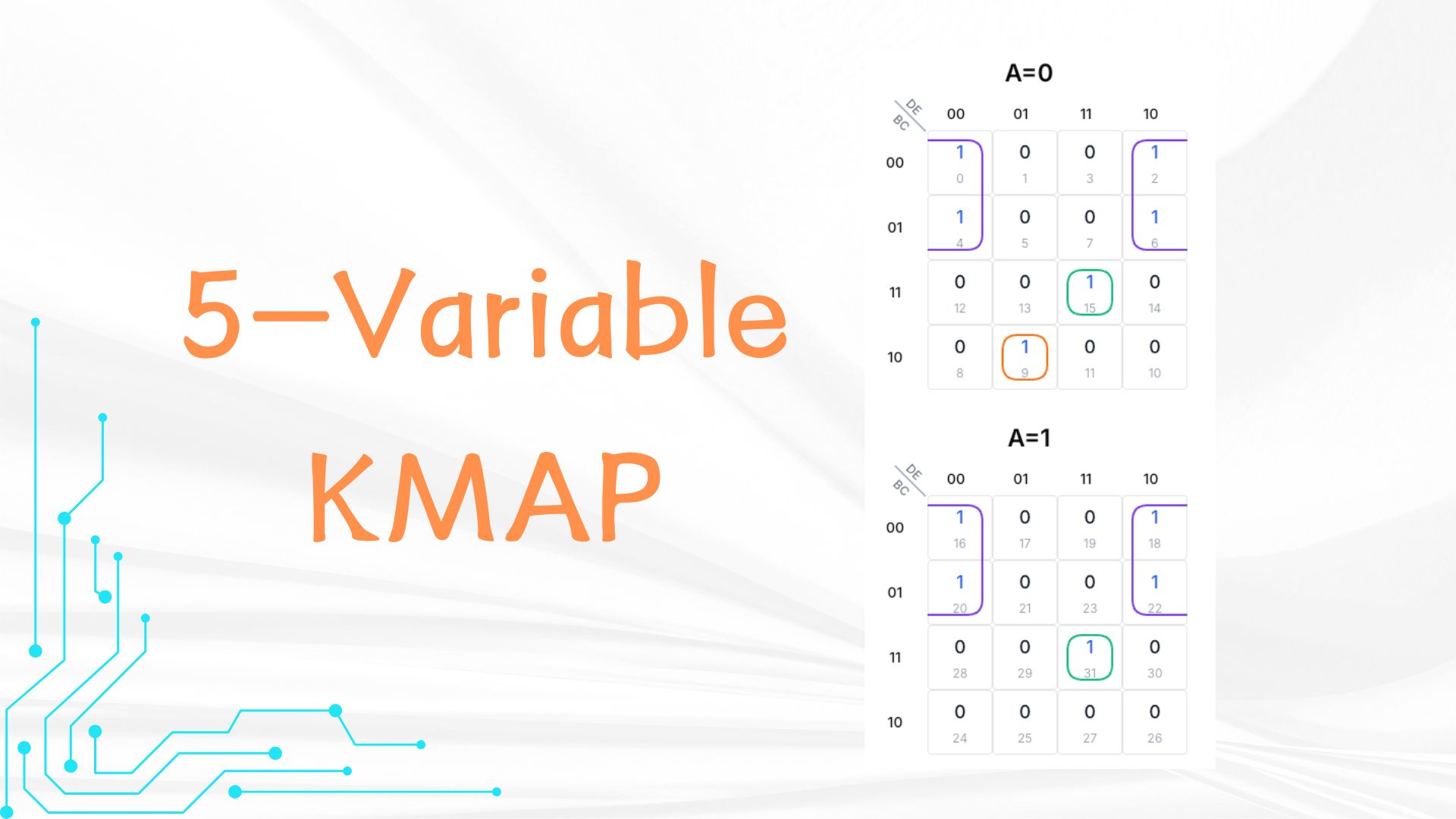
Considera l'espressione: A'B'C'D'E' + A'B'C'DE' + A'B'CD'E' + A'B'CDE' + A'BC'D'E + A'BCDE + AB'C'D'E' + AB'C'DE' + AB'CD'E' + AB'CDE' + ABCDE. In binario: celle 0,2,4,6,9,15,16,18,20,22,31.
Step 1: Compilazione K-Map
Nella griglia A=0 (B,C come righe, D,E colonne in codice Gray):
- Riga 00 (B=0,C=0), colonna 00 (D=0,E=0): 1
- Riga 00, colonna 01 (D=1,E=0): 1
- Riga 01 (B=0,C=1), colonna 11 (D=0,E=0): 1
- Riga 01, colonna 10 (D=1,E=0): 1
- Riga 11 (B=1,C=1), colonna 11 (D=1,E=1): 1
- Riga 10 (B=1,C=0), colonna 01 (D=0,E=1): 1
In the A=1 grid, rows are also B and C (00, 01, 11, 10), columns are also D and E (00, 01, 11, 10). Put 1s:
- Riga 00, colonna 00: 1
- Riga 00, colonna 01: 1
- Riga 01, colonna 11: 1
- Riga 01, colonna 10: 1
- Riga 11, colonna 11: 1

Step 2: Raggruppamento
11 celle attive: 6 in A=0, 5 in A=1.
- Gruppo 1: Termine singolo A'BC'D'E
- Gruppo 2: 8 termini con B' ed E' costanti
- Gruppo 3: A'BCDE + ABCDE

Step 3: Semplificazione
- Gruppo 1: Mantieni A'BC'D'E
- Gruppo 2: B' ed E' costanti → B'E'
- Gruppo 3: A irrilevante → BCDE
Espressione semplificata: A'BC'D'E + B'E' + BCDE

Consigli per Padroneggiare le K-Map 5V
Errori Comuni da Evitare
- Etichette errate: Non usare codice Gray
- Connessioni mancanti: Dimenticare l'adiacenza tra griglie
- Gruppi non validi: Celle non adiacenti
- Gruppi troppo piccoli: Non sfruttare dimensioni massime
- Termini errati: Variabili non costanti nel gruppo
Best Practice per Efficienza
- Usa sempre codice Gray per righe/colonne
- Cerca prima i gruppi più ampi
- Verifica coppie tra A=0 e A=1
- Assicura copertura totale degli 1
- Verifica termini con controllo incrociato
Metti in pratica queste conoscenze con il nostro Strumento Interattivo per K-Map che supporta fino a 5 variabili. Uno strumento ideale per verificare i tuoi progressi e acquisire sicurezza. Con la pratica, diventerà semplice come usare una K-Map a 4 variabili!