5-वेरिएबल K-Map हल करें: चरण-दर-चरण सरलीकरण गाइड

कर्नॉफ मैप (K-Map) क्या है?

क्या आपने कभी सोचा है कंप्यूटर निर्णय कैसे लेते हैं? वे बूलियन लॉजिक का उपयोग करते हैं, जो सही और गलत मूल्यों से संबंधित है। जब हम इन सही-गलत कथनों को जोड़ते हैं, तो ये काफी जटिल हो सकते हैं। यहीं कर्नॉफ मैप (K-Map) काम आता है। K-Map एक सरल टूल है जो इन लॉजिकल कथनों को एक सुव्यवस्थित ग्रिड में व्यवस्थित करता है। यह ग्रिड वेरिएबल्स के हर संभव संयोजन को दर्शाता है, जिससे हम पैटर्न आसानी से पहचान सकते हैं। इन पैटर्न्स को पहचानकर हम लॉजिक को सरल बना सकते हैं।

यदि आप K-Map के बारे में अधिक जानना चाहते हैं या 4-वेरिएबल K-Map को हल करना सीखना चाहते हैं, तो विस्तृत जानकारी के लिए रेफरेंस आर्टिकल देखें: 4-वेरिएबल K-Map को कैसे हल करें

पाँच-वेरिएबल K-Map क्यों उपयोग करें?

अधिकांश K-Map दो, तीन या चार वेरिएबल्स को हैंडल करते हैं। लेकिन कभी-कभी हमें पाँच वेरिएबल्स वाली जटिल समस्याओं का सामना करना पड़ता है। कल्पना करें पाँच स्विच वाला सर्किट डिज़ाइन करना - प्रत्येक स्विच चालू या बंद हो सकता है। यह संभावित संयोजनों की भारी संख्या है! पाँच-वेरिएबल K-Map इस जटिलता को प्रबंधित करने में मदद करता है। यह उन एक्सप्रेशन्स को सरल बनाता है जिन्हें अन्यथा हैंडल करना मुश्किल होता। चाहे आप कोई गैजेट बना रहे हों या प्रोग्राम कोडिंग कर रहे हों, पाँच-वेरिएबल K-Map आपका समय और मेहनत बचा सकता है।

लेआउट और वेरिएबल असाइनमेंट

पाँच-वेरिएबल K-Map जटिल लग सकता है, लेकिन यह आपके ज्ञात चार-वेरिएबल K-Map का ही विस्तार है। चार-वेरिएबल K-Map एक 4x4 ग्रिड होता है जिसमें 16 सेल होते हैं। प्रत्येक सेल चार वेरिएबल्स (जैसे B,C,D,E) के संयोजन को दर्शाता है। पंक्तियों में B और C, जबकि कॉलम में D और E होते हैं। अब पाँचवें वेरिएबल A को जोड़ें। सभी 32 संयोजनों (2⁵ = 32) को समायोजित करने के लिए, हम दो 4x4 ग्रिड्स को साथ-साथ रखते हैं। एक ग्रिड A=0 के लिए और दूसरा A=1 के लिए। प्रत्येक ग्रिड में पंक्तियाँ अभी भी B और C, और कॉलम D और E ही रहते हैं। यह सेटअप अतिरिक्त वेरिएबल को हैंडल करते हुए परिचित संरचना बनाए रखता है।

5-वेरिएबल K-Map की मूल संरचना, दो 4x4 ग्रिड दिखाते हुए

चार-वेरिएबल K-Map से अंतर

तो पाँच-वेरिएबल K-Map कैसे अलग है? आइए मुख्य अंतरों को समझें:

• अधिक सेल: पाँचवें वेरिएबल के कारण 16 के बजाय 32 सेल
• दोहरी ग्रिड संरचना: A=0 और A=1 को अलग-अलग ग्रिड में रखा जाता है
• क्रॉस-ग्रिड निकटता: सेल अलग-अलग ग्रिड्स में भी पड़ोसी हो सकते हैं। उदाहरण के लिए, A=0 ग्रिड का सेल A=1 ग्रिड के समान स्थान वाले सेल का पड़ोसी होता है
• बड़े समूह: हम 32 सेल तक के समूह बना सकते हैं, हालाँकि छोटे समूह अधिक सामान्य हैं

चिंता न करें - समूह बनाने की मूल अवधारणा वही रहती है

चरण 1: चर निर्धारित करें

पाँच चरों (A,B,C,D,E) से शुरुआत करें। ये किसी भी स्विच या सर्किट को प्रदर्शित कर सकते हैं। आपका कार्य यह निर्धारित करना है कि इन चरों के सभी संयोजनों के लिए आपका बूलियन फलन सत्य (1) या असत्य (0) कब होता है।

चरण 2: पंक्तियों और स्तंभों को लेबल करें

दो 4x4 ग्रिड तैयार करें। दोनों ग्रिड की पंक्तियों को B और C से लेबल करें (ग्रे कोड क्रम में: 00, 01, 11, 10)। स्तंभों को D और E से ग्रे कोड क्रम में लेबल करें। बाएँ ग्रिड को A=0 और दाएँ ग्रिड को A=1 के रूप में चिह्नित करें। अब आपका मैप तैयार है!

चरण 3: फलन मानों से सेल भरें

प्रत्येक A,B,C,D,E संयोजन के लिए फलन मान जांचें। A=0 होने पर बाएँ ग्रिड में B/C पंक्ति और D/E स्तंभ पर मान रखें। A=1 होने पर दाएँ ग्रिड में समान स्थान पर मान भरें। सभी 32 सेल भरने तक जारी रखें। "मिनटर्म" सूची होने पर उन सेल में 1 और बाकी में 0 भरें।

समूहन के नियम

K-Map में 1 को समूहित करके सरलीकरण करें। नियम:

• समूह का आकार दो की घात होना चाहिए: 1, 2, 4, 8, 16 या 32
• समूह वर्गाकार/आयताकार होने चाहिए (जैसे 2x2 या 1x4)
• समूह के सभी सेल सन्निकट होने चाहिए (निकटता की व्याख्या आगे)
• अधिकतम संभव आकार के समूह बनाएं
• प्रत्येक 1 कम से कम एक समूह में हो, परंतु एकाधिक समूहों में हो सकता है

पाँच चर K-Map में मान्य समूहन का उदाहरण

सन्निकट सेलों की पहचान

सेल "सन्निकट" हैं यदि वे केवल एक चर में भिन्न हों। प्रत्येक ग्रिड में क्षैतिज/ऊर्ध्वाधर पड़ोसी सेल सन्निकट हैं। A=0 ग्रिड का सेल A=1 ग्रिड के समान स्थान वाले सेल से भी सन्निकट है (केवल A बदलता है)। यह समूहों को दोनों ग्रिड में फैलाने देता है।

पाँच चरों में व्रैप-अराउंड प्रबंधन

K-Map में किनारे जुड़े होते हैं: शीर्ष पंक्ति निचली से, बायाँ स्तंभ दायें से जुड़ा होता है। A=0 और A=1 ग्रिड के सेल भी समान स्थान पर जुड़े होते हैं। इससे ग्रिडों के बीच समूह बनाना संभव है। यह मैप को विशेष तरीके से मोड़ने जैसा है जो अधिक सन्निकटता खोजने में मदद करता है।

पाँच चर K-Map में सन्निकट सेलों का उदाहरण - समान रंग की सीमा वाले सेल एक समूह में हैं

प्राइम इम्प्लिकेंट्स की पहचान

प्राइम इम्प्लिकेंट 1s का एक समूह होता है जो अपने अधिकतम संभव आकार में होता है। नियमों का उपयोग करके सभी संभावित 1s के समूह ढूंढ़कर शुरू करें। फिर जांचें कि कोई भी समूह किसी अन्य समूह के साथ मिलकर बड़ा नहीं बन सकता। ये अधिकतम समूह आपके प्राइम इम्प्लिकेंट्स होते हैं - ये आपके सरलीकृत एक्सप्रेशन के मूलभूत घटक हैं।

आवश्यक प्राइम इम्प्लिकेंट्स का चयन

कुछ प्राइम इम्प्लिकेंट्स अनिवार्य होते हैं। उन 1s को ढूंढ़ें जो केवल एक समूह से संबंधित हैं। वह समूह "आवश्यक" होता है क्योंकि उस 1 को कवर करने के लिए आपको इसकी आवश्यकता होती है। सबसे पहले सभी आवश्यक समूहों को शामिल करें। यदि कोई 1s अभी भी अनकवर रह जाते हैं, तो उन्हें कवर करने के लिए अतिरिक्त समूह चुनें। उन समूहों को प्राथमिकता दें जो सबसे अधिक बचे हुए 1s को कम से कम समूहों में कवर करते हैं।

न्यूनतम एक्सप्रेशन लिखना

प्रत्येक समूह आपको एक टर्म देता है। यहां बताया गया है कैसे:

• समूह में स्थिर रहने वाले चरों की पहचान करें।
• यदि कोई चर हमेशा 1 रहता है, उसे शामिल करें (जैसे B)।
• यदि हमेशा 0 रहता है, उसके इनवर्स को शामिल करें (जैसे B' "नॉट B")।
• उन चरों को छोड़ दें जो समूह के भीतर बदलते हैं।

इन टुकड़ों के AND के रूप में प्रत्येक टर्म लिखें। फिर आपका अंतिम एक्सप्रेशन सभी चयनित समूहों के टर्म्स का OR होगा। यही आपका सरलीकृत बूलियन एक्सप्रेशन है!

5-चर K-Map से सरलीकृत एक्सप्रेशन का उदाहरण

एक उदाहरण आज़माते हैं। मान लीजिए यह बूलियन एक्सप्रेशन है: A'B'C'D'E' + A'B'C'DE' + A'B'CD'E' + A'B'CDE' + A'BC'D'E + A'BCDE + AB'C'D'E' + AB'C'DE' + AB'CD'E' + AB'CDE' + ABCDE. बाइनरी में, ये सेल्स हैं 00000 (0), 00010 (2), 00100 (4), 00110 (6), 01001 (9), 01111 (15), 10000 (16), 10010 (18), 10100 (20), 10110 (22), 11111 (31)।

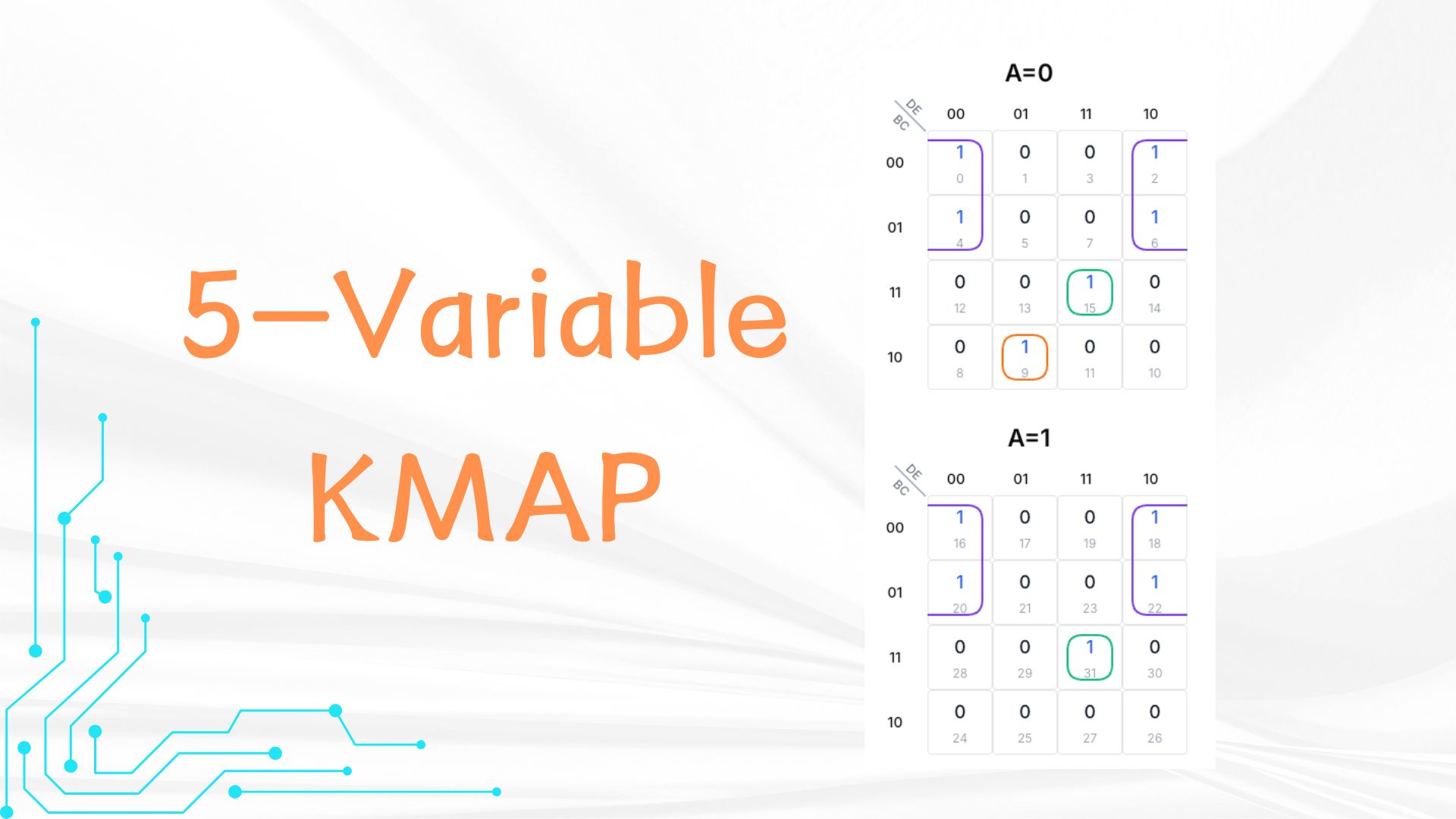
चरण 1: K-Map भरें

A=0 ग्रिड में, पंक्तियां B और C (00, 01, 11, 10), कॉलम D और E (00, 01, 11, 10) हैं। 1s रखें:

• पंक्ति 00 (B=0, C=0), कॉलम 00 (D=0, E=0): 1
• पंक्ति 00 (B=0, C=0), कॉलम 01 (D=1, E=0): 1
• पंक्ति 01 (B=0, C=1), कॉलम 11 (D=0, E=0): 1
• पंक्ति 01 (B=0, C=1), कॉलम 10 (D=1, E=0): 1
• पंक्ति 11 (B=1, C=1), कॉलम 11 (D=1, E=1): 1
• पंक्ति 10 (B=1, C=0), कॉलम 01 (D=0, E=1): 1

In the A=1 grid, rows are also B and C (00, 01, 11, 10), columns are also D and E (00, 01, 11, 10). Put 1s:

• पंक्ति 00 (B=0, C=0), कॉलम 00 (D=0, E=0): 1
• पंक्ति 00 (B=0, C=0), कॉलम 01 (D=1, E=0): 1
• पंक्ति 01 (B=0, C=1), कॉलम 11 (D=0, E=0): 1
• पंक्ति 01 (B=0, C=1), कॉलम 10 (D=1, E=0): 1
• पंक्ति 11 (B=1, C=1), कॉलम 11 (D=1, E=1): 1

5-चर K-Map से सरलीकृत एक्सप्रेशन का उदाहरण

चरण 2: 1s को समूहित करें

हमारे पास ग्यारह 1s हैं: छह A=0 ग्रिड में और पांच A=1 ग्रिड में।

• समूह 1: एकल पद - A'BC'D'E।
• समूह 2: A'B'C'D'E' + A'B'C'DE' + A'B'CD'E' + A'B'CDE' + AB'C'D'E' + AB'C'DE' + AB'CD'E' + AB'CDE'।
• समूह 3: A'BCDE + ABCDE।

5-चर K-Map से सरलीकृत एक्सप्रेशन का उदाहरण

चरण 3: सरलीकरण

• समूह 1: एकल पद रखें - A'BC'D'E।
• समूह 2: केवल B' और E' स्थिर हैं, इसलिए B'E' रखें।
• समूह 3: केवल A बदलता है जिसका अर्थ है यह एक्सप्रेशन के लिए अप्रासंगिक, इसलिए BCDE रखें।

अतः सरलीकृत एक्सप्रेशन है: A'BC'D'E + B'E' + BCDE

5-चर K-Map से सरलीकृत एक्सप्रेशन का उदाहरण

इन सामान्य गलतियों से बचें

• गलत लेबलिंग: ग्रे कोड का उपयोग न करने से पड़ोसी सेल्स का संबंध गड़बड़ हो जाता है।
• कनेक्शन छूटना: ग्रिड्स के पार सेल जोड़े बनाना भूल जाना।
• खराब समूहन: गैर-आसन्न सेल्स को समूहित करना।
• छोटे समूह: संभावित सबसे बड़े समूह न बनाना।
• गलत टर्म्स: समूह में स्थिर रहने वाले चरों को मिलाने की भूल।

कुशलता के लिए सर्वोत्तम अभ्यास

• हमेशा पंक्तियों और स्तंभों के लिए ग्रे कोड का उपयोग करें।
• सबसे बड़े समूह पहले ढूंढें - ये अधिकतम सरलीकरण करते हैं।
• A=0 और A=1 ग्रिड्स में पार के जोड़े जांचें।
• सुनिश्चित करें कि हर 1 किसी समूह में शामिल हो।
• अपने टर्म्स को ग्रिड से मिलाकर दोबारा जांचें।

इन चरणों, उदाहरणों और टिप्स के साथ आप पांच चर वाले K-Maps को विशेषज्ञ की तरह हल करने के लिए तैयार हैं! अभ्यास के लिए हमारे इंटरएक्टिव K-Map सॉल्वर टूल का उपयोग करें जो 5 चरों तक सपोर्ट करता है। यह आपके काम की जांच करने और K-Maps हल करने में आत्मविश्वास बनाने का शानदार तरीका है। निरंतर अभ्यास से यह चार-चर वाले K-Map जितना आसान लगने लगेगा।