Solve 5-Variable K-Maps: Your Step-by-Step Simplification Guide

What is a Karnaugh Map?

Have you ever wondered how computers make decisions? They use something called Boolean logic, which deals with true and false values. These true and false statements can get pretty tricky when we combine them. That's where a Karnaugh Map, or K-Map, steps in to save the day. A K-Map is an easy tool that puts these logical statements into a neat grid. The grid lays out every possible mix of variables, so we can quickly see patterns. Spotting these patterns helps us make the logic simpler.

If you want to dig deeper into what a K-Map is or how to solve a 4-variable K-Map, check out the reference article for more details: How to Solve a 4-Variable K-Map

Why Use a Five-Variable K-Map?

Most K-Maps handle two, three, or four variables. But sometimes, we face bigger challenges with five variables. Imagine designing a circuit with five switches—each switch can be on or off. That's a lot of combinations to figure out! A five-variable K-Map helps us manage this complexity. It lets us simplify expressions that would be tough to handle otherwise. Whether you're building a gadget or coding a program, a five-variable K-Map can save you time and effort.

Layout and Variable Assignment

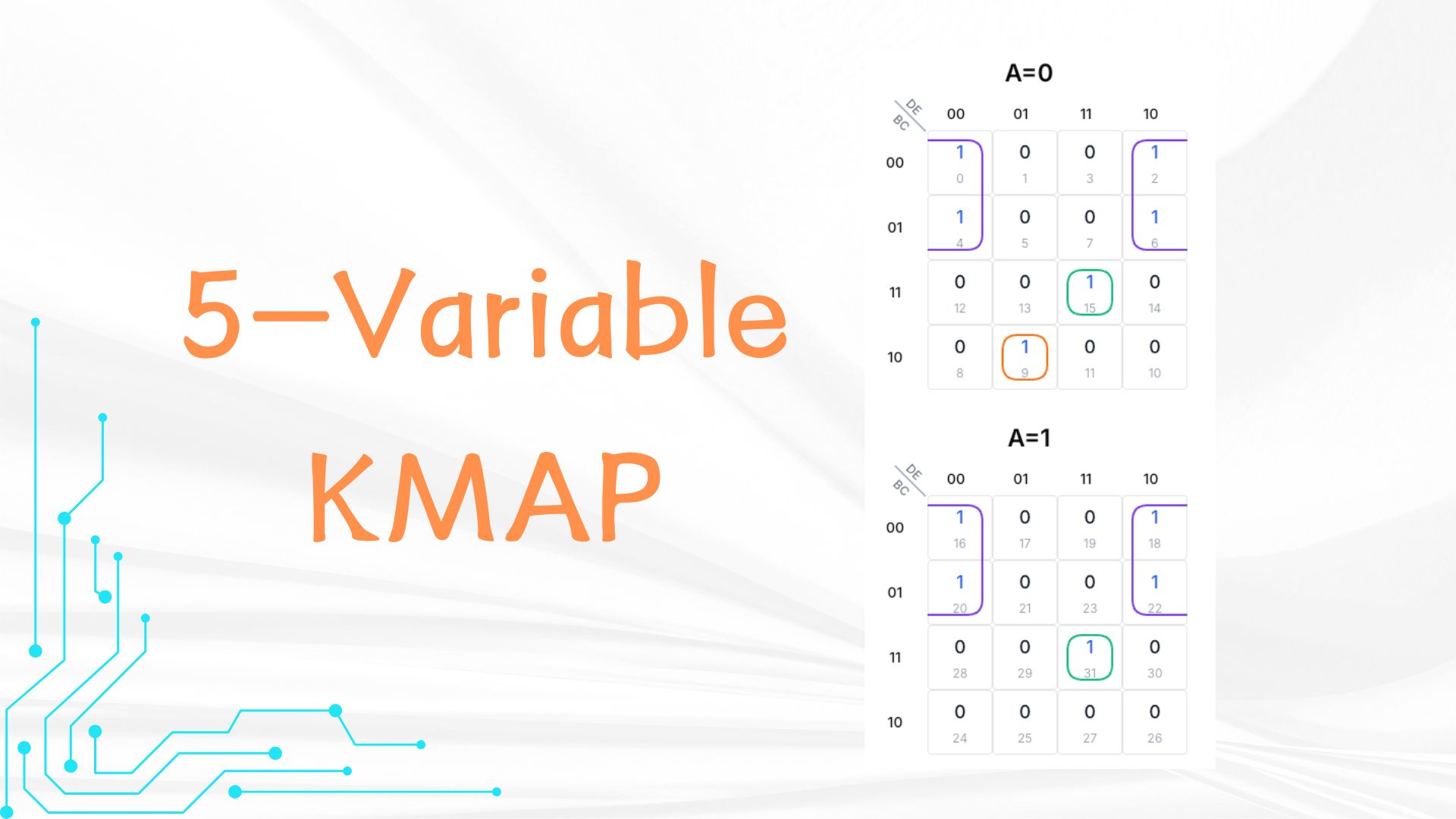
A five-variable K-Map might sound complicated, but it's just an extension of what you may already know. Picture a four-variable K-Map: it's a 4x4 grid with 16 cells. Each cell represents a combination of four variables, like B,C,D,E. The rows use B and C, and the columns use D and E. Now, add a fifth variable, A. To fit all 32 combinations (since 2⁵ = 32), we use two 4x4 grids side by side. One grid is for when A is 0, and the other is for when A is 1. In each grid, the rows are still B and C, and the columns are D and E. This setup keeps things familiar while handling the extra variable.

Basic structure of a 5-variable K-Map showing two 4x4 grids

Differences from Four-Variable K-Maps

So, how is a five-variable K-Map different? Let's break down the key differences:

• More Cells: It has 32 cells instead of 16 because of that fifth variable.
• Dual Grid Structure: We use two grids to account for A being 0 or 1.
• Cross-Grid Adjacency: Cells can be "next to" each other between the grids. For example, a cell in the A=0 grid is neighbors with the same spot in the A=1 grid.
• Larger Groups: We can make larger groups, up to 32 cells, though smaller ones are more common.

Don't worry—the basic idea of grouping stays the same.

Step 1: Determine the Variables

Start with your five variables. Let's call them A,B,C,D,E. These could represent anything, like switches in a circuit. Your job is to figure out when your Boolean function is true (1) or false (0) for all combinations of these variables.

Step 2: Label the Rows and Columns

Next, set up your two 4x4 grids. Label the rows in both grids with B and C. Use a special order called Gray code, where each step changes only one bit: 00, 01, 11, 10. This keeps neighbors close in the logic. Then, label the columns in both grids with D and E, also in Gray code: 00, 01, 11, 10. Finally, mark the left grid as A=0 and the right grid as A=1. Now your map is ready!

Step 3: Fill in the Cells with Function Values

Time to add your function's values. For each combination of A,B,C,D,E, check if the function is 1 or 0. If A is 0, put the value in the left grid at the row for B and C and the column for D and E. If A is 1, put it in the right grid at the same spot. Keep going until all 32 cells are filled. If you have a list of "minterms" (combinations where the function is 1), just place 1s in those cells and 0s everywhere else.

Rules for Grouping

Simplifying happens by grouping 1s in the K-Map. Here are the rules:

• Groups must be a size that's a power of two: 1, 2, 4, 8, 16, or 32.
• Groups should be square or rectangular, like 2x2 or 1x4.
• All cells in a group must be next to each other (we'll explain "next to" soon).
• Make groups as big as possible for the best simplification.
• Every 1 must be in at least one group, but it's fine if some 1s are in multiple groups.

Example of valid groupings in a 5-variable K-Map

Identifying Adjacent Cells

Cells are "adjacent" if they differ in just one variable. In each grid, cells next to each other horizontally or vertically are adjacent. Plus, a cell in the A=0 grid is adjacent to the same spot in the A=1 grid because only A changes. For example, row 00, column 00 with A=0 is neighbors with row 00, column 00 with A=1. This lets groups stretch across both grids.

Handling Wrap-Arounds in Five Variables

K-Maps have a cool trick: edges wrap around. In each grid, the top row connects to the bottom row, and the left column connects to the right column. Also, because of the two grids, cells can connect between A=0 and A=1. This means you can group cells across grids if they're in the same position. It's like the map folds in a special way to help you find more neighbors.

Example of adjacent cells in a 5-variable K-Map, cells with the same color border belong to the same group

Finding Prime Implicants

A prime implicant is a group of 1s that's as big as it can get. Start by finding all possible groups of 1s using the rules. Then, check that each group can't join with another to make a bigger one. These maximal groups are your prime implicants—they're the building blocks of your simplified expression.

Selecting Essential Prime Implicants

Some prime implicants are must-haves. Look for 1s that only belong to one group. That group is "essential" because you need it to cover that 1. Include all essential groups first. Then, if any 1s are still uncovered, pick extra groups to cover them. Choose ones that cover the most leftover 1s with the fewest groups.

Writing the Minimal Expression

Each group gives you a term. Here's how:

• Find which variables stay the same in the group.
• If a variable is always 1, include it (like B).
• If it's always 0, include its opposite (like B' for "not B").
• Skip variables that change within the group.

Write each term as an AND of these pieces. Then, your final expression is the OR of all the terms from your selected groups. That's your simplified Boolean expression!

Example of a simplified expression from a 5-variable K-Map

Let's try an example. Suppose this boolean expression: A'B'C'D'E' + A'B'C'DE' + A'B'CD'E' + A'B'CDE' + A'BC'D'E + A'BCDE + AB'C'D'E' + AB'C'DE' + AB'CD'E' + AB'CDE' + ABCDE. In binary, that's cells 00000 (0), 00010 (2), 00100 (4), 00110 (6), 01001 (9), 01111 (15), 10000 (16), 10010 (18), 10100 (20), 10110 (22), 11111 (31).

Step 1: Fill the K-Map

In the A=0 grid, rows are B and C (00, 01, 11, 10), columns are D and E (00, 01, 11, 10). Put 1s:

• Row 00 (B=0, C=0), column 00 (D=0, E=0): 1
• Row 00 (B=0, C=0), column 01 (D=1, E=0): 1
• Row 01 (B=0, C=1), column 11 (D=0, E=0): 1
• Row 01 (B=0, C=1), column 10 (D=1, E=0): 1
• Row 11 (B=1, C=1), column 11 (D=1, E=1): 1
• Row 10 (B=1, C=0), column 01 (D=0, E=1): 1

In the A=1 grid, rows are also B and C (00, 01, 11, 10), columns are also D and E (00, 01, 11, 10). Put 1s:

• Row 00 (B=0, C=0), column 00 (D=0, E=0): 1
• Row 00 (B=0, C=0), column 01 (D=1, E=0): 1
• Row 01 (B=0, C=1), column 11 (D=0, E=0): 1
• Row 01 (B=0, C=1), column 10 (D=1, E=0): 1
• Row 11 (B=1, C=1), column 11 (D=1, E=1): 1

Example of a simplified expression from a 5-variable K-Map

Step 2: Group the 1s

We have eleven 1s: six in the A=0 grid and five in the A=1 grid.

• Group 1: Single term: A'BC'D'E.
• Group 2: A'B'C'D'E' + A'B'C'DE' + A'B'CD'E' + A'B'CDE' + AB'C'D'E' + AB'C'DE' + AB'CD'E' + AB'CDE'.
• Group 3: A'BCDE + ABCDE.

Example of a simplified expression from a 5-variable K-Map

Step 3: Simplify

• Group 1: Keep Single term: A'BC'D'E.
• Group 2: Only B' and E' are constant, so we keep B'E'.
• Group 3: Only A changes which means it's irrelevant to the expression, so we keep BCDE.

So, the simplified expression is: A'BC'D'E + B'E' + BCDE

Example of a simplified expression from a 5-variable K-Map

Common Mistakes to Avoid

• Wrong Labels: Not using Gray code messes up who's next to whom.
• Missing Connections: Forgetting cells can pair across grids.
• Bad Groups: Grouping cells that aren't adjacent.
• Small Groups: Not making the biggest groups possible.
• Wrong Terms: Mixing up which variables stay the same in a group.

Best Practices for Efficiency

• Always use Gray code for rows and columns.
• Look for big groups first—they simplify the most.
• Check both grids for pairs across A=0 and A=1.
• Make sure every 1 is in a group.
• Double-check your terms by matching them to the grid.

With these steps, examples, and tips, you're ready to tackle five-variable K-Maps like a pro! To put your knowledge into practice, try our interactive K-Map Solver Tool that supports up to 5 variables. It's a great way to check your work and build confidence in solving K-Maps. Keep practicing, and it'll feel as easy as a four-variable one.