كيفية حل خريطة K-Map رباعية المتغيرات: دليل تفصيلي خطوة بخطوة
ما هي خريطة كارنو (K-Map) ودورها في المنطق الرقمي
خريطة كارنو (K-Map) هي أداة تُستخدم لتبسيط التعبيرات المنطقية في الدوائر الرقمية. تعمل هذه التعبيرات كتعليمات للدوائر الرقمية باستخدام قيم الصواب والخطأ لتحويل المدخلات إلى مخرجات. يساعد تبسيطها في جعل الدوائر أصغر حجمًا وأسرع أداءً وأقل تكلفة.
تستخدم خريطة كارنو شبكة من المربعات لهذا الغرض. في الخريطة رباعية المتغيرات تحتوي على 16 مربعًا. يمثل كل مربع تركيبة فريدة من أربعة مدخلات، حيث تختلف المربعات المجاورة بمتغير واحد فقط. هذا التصميم يساعد في اكتشاف الأنماط وتجميع المخرجات المتشابهة لتبسيط التعبير.
تتميز خرائط كارنو بكونها بصرية وسهلة الاستخدام، حيث تفوق الطرق الرياضية البحتة في تقليل الأخطاء. تعمل بشكل أفضل مع أربعة أو خمسة متغيرات، مما يتناسب مع معظم تصميمات الدوائر العملية.
أُدخلت خرائط كارنو بواسطة موريس كارنو عام 1953 بناءً على أعمال إدوارد فيتش، وأصبحت منذ ذلك الحين أداة أساسية في تصميم الدوائر الرقمية.
إعداد خريطة كارنو رباعية المتغيرات
فهم الشبكة وتعيين المتغيرات
تبدأ خريطة كارنو رباعية المتغيرات بشبكة 4×4 تحتوي على 16 مربعًا، كل منها يمثل تركيبة محتملة من أربعة مدخلات: A، B، C، D. تُعرِّف الصفوف بأزواج من A وB على الجانب، بينما تُعرِّف الأعمدة بأزواج من C وD في الأعلى. يتم ملء كل مربع بقيمة 1 أو 0 حسب المشكلة المنطقية، مما يحول المشكلة إلى صورة قابلة للتبسيط.

أهمية كود جراي في خرائط كارنو
في الخريطة رباعية المتغيرات، لا تتبع تسميات الصفوف والأعمدة التسلسل الثنائي العادي (00، 01، 10، 11)، بل تستخدم كود جراي: 00، 01، 11، 10. يتميز كود جراي بتغيير بت واحد فقط في كل خطوة، مما يسهل عملية التجميع.
هذا الأمر بالغ الأهمية، حيث تختلف المربعات المجاورة بمتغير واحد فقط بفضل كود جراي، مما يجعل عملية تجميع المربعات المتشابهة أكثر كفاءة في تبسيط التعبير.
الكود الثنائي
كود جراي
رسم الدالة
تحويل الدالة المنطقية إلى مصطلحات مينتيرم
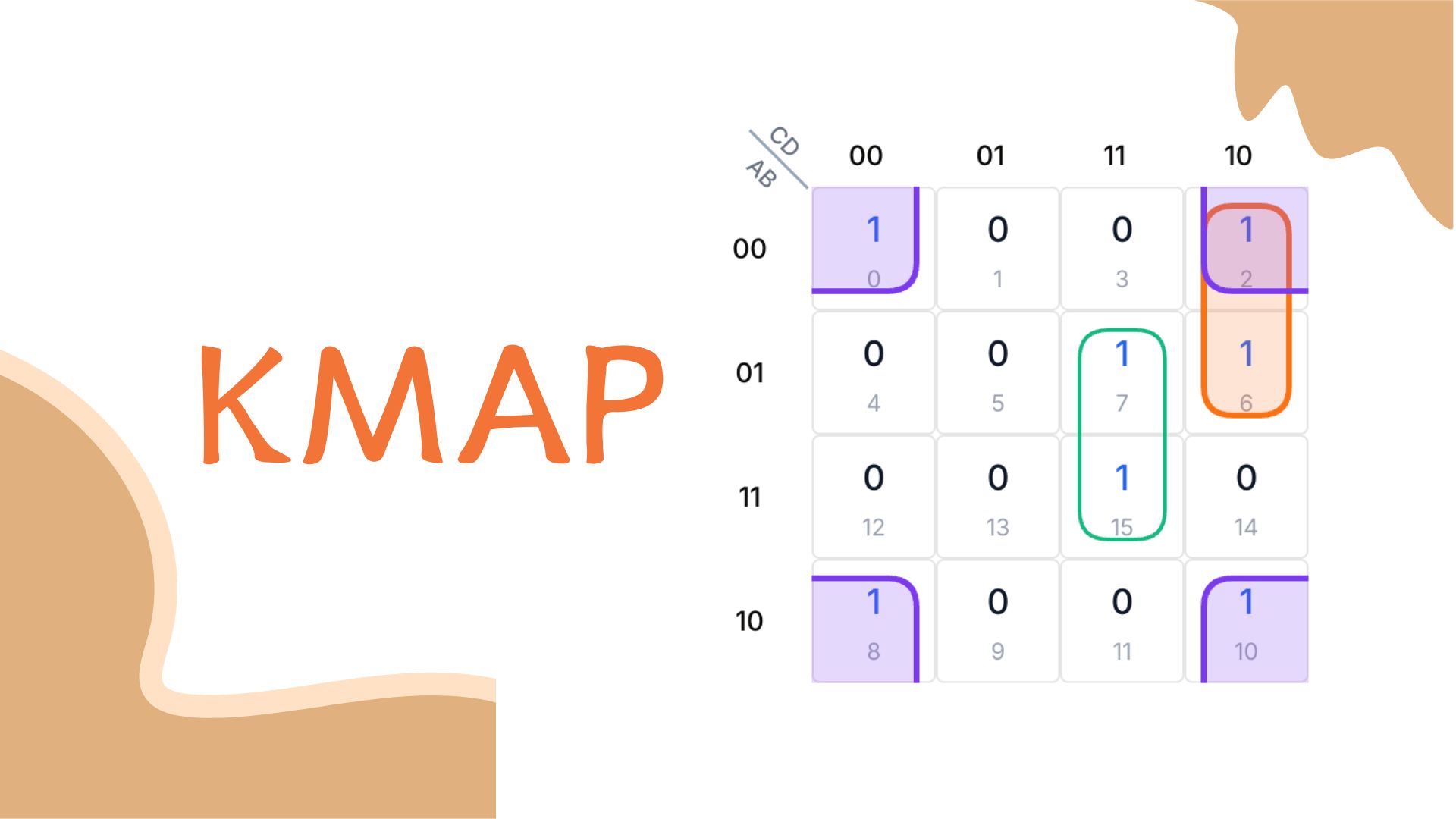
للاستفادة من خريطة كارنو، نحدد التركيبات التي تجعل الدالة المنطقية صحيحة (قيمة 1)، والتي تسمى مصطلحات مينتيرم. على سبيل المثال، في الدالة F = A'B'C'D' + A'B'CD' + A'BC'D + A'BCD + AB'C'D' + AB'CD'، تتوافق كل حدية مع مصطلحات مينتيرم 0، 2، 5، 7، 8، و10.
F(A,B,C,D) = A'B'C'D' + A'B'CD' + A'BC'D + A'BCD + AB'C'D' + AB'CD'
= Σm(0,2,5,7,8,10)
رسم مصطلحات مينتيرم على خريطة كارنو
نقوم بوضع علامة 1 في المربعات المرتبطة بمصطلحات مينتيرم المحددة (0، 2، 5، 7، 8، 10) بينما تبقى المربعات الأخرى 0.

تبسيط الدالة
تقنيات التجميع: الحجم، الشكل، والموقع
بعد رسم مصطلحات مينتيرم، نقوم بتجميع الوحدات (1s) بناءً على ثلاثة معايير: الحجم، الشكل المستطيل، والموقع الأمثل لتغطية أكبر عدد من الوحدات بأقل المجموعات.
الحجم: اختر أكبر مجموعة ممكنة
نهدف لتكوين مجموعات كبيرة (2، 4، أو 8 وحدات) لتقليل عدد الحديات في التعبير النهائي.
الشكل: التزم بالمستطيلات
يجب أن تكون المجموعات مستطيلة الشكل (صفوف، أعمدة، أو كتل) لضمان تبسيط فعال وفق قواعد خرائط كارنو.
الموقع: استخدم الشبكة بذكاء
يمكن أن تمتد المجموعات عبر الحواف أو تتداخل لتحقيق أفضل تغطية للوحدات.

مجموعة من 2

مجموعة من 4
حالات الحواف والمجموعات الملتفة
تسمح خرائط كارنو بتجميع الوحدات عبر الحواف المتقابلة بفضل خاصية الالتفاف، مما يتيح تكوين مجموعات غير تقليدية.
الحواف المتصلة
يمكن تجميع الوحدات في الحواف العلوية والسفلية أو الجانبية كمجموعة واحدة بسبب خاصية الالتفاف.
الزوايا المتصلة
تمكن خاصية الالتفاف من تجميع الوحدات في الزوايا الأربع كمجموعة واحدة.

مجموعة أفقية

مجموعة حافة
اشتقاق التعبير المبسط
تحليل المجموعات لتكوين حديات الضرب
نستخرج من كل مجموعة حدية ضرب تحتوي على المتغيرات الثابتة فقط، مع إهمال المتغيرات المتغيرة داخل المجموعة.
مجموعة من مربعين
مثال: AB'D من مجموعة مكونة من مربعين حيث يتغير المتغير C.

مجموعة من مربعين

مجموعة من مربعين مبسطة
مجموعة من أربعة مربعات
مثال: BD من مجموعة 2x2 حيث يتغير المتغيران A وC.

مجموعة من أربعة مربعات

مجموعة من أربعة مربعات مبسطة
مجموعة من ثمانية مربعات
مثال: A' من مجموعة تغطي نصف الخريطة حيث يتغير B، C، وD.

مجموعة من ثمانية مربعات

مجموعة من ثمانية مربعات مبسطة
كيف يعمل التبسيط
يتم التبسيط من خلال إهمال المتغيرات المتغيرة داخل المجموعة، والاحتفاظ بالثوابت فقط لتكوين حديات أقصر.
بناء التعبير النهائي بصيغة SOP
نجمع حديات الضرب الناتجة باستخدام علامات الجمع للحصول على التعبير المبسط بصيغة جمع الحديات (SOP).
استراتيجيات التجميع المتقدمة
متى نستخدم المجموعات المتداخلة
يمكن أن تنتمي الوحدة إلى أكثر من مجموعة إذا ساهم ذلك في تقليل عدد الحديات النهائية.
مثال: مشاركة وحدة في مجموعة أفقية وعمودية لتحقيق تبسيط أفضل.

مجموعة متداخلة
الختام
ملخص عملية تبسيط خريطة كارنو
عملية التبسيط تشبه حل لغز: إعداد الشبكة، رسم الوحدات، التجميع الذكي باستخدام أكبر المجموعات الممكنة مع مراعاة الالتفاف، ثم اشتقاق التعبير من الحديات الثابتة.
النقاط الرئيسية
- 1فهم بنية الشبكة وتعيين المتغيرات
- 2رسم مصطلحات مينتيرم بدقة
- 3تكوين أكبر مجموعات مستطيلة ممكنة
- 4اشتقاق التعبير المبسط من المجموعات
موارد لمزيد من الممارسة
تدرب باستخدام أدوات تفاعلية لحل خرائط كارنوف التي توضح عملية التبسيط. جرب أداة حل خرائط كارنوف الخاصة بنا للتجربة مع تعبيراتك المنطقية الخاصة.